고귀양이의 노트.

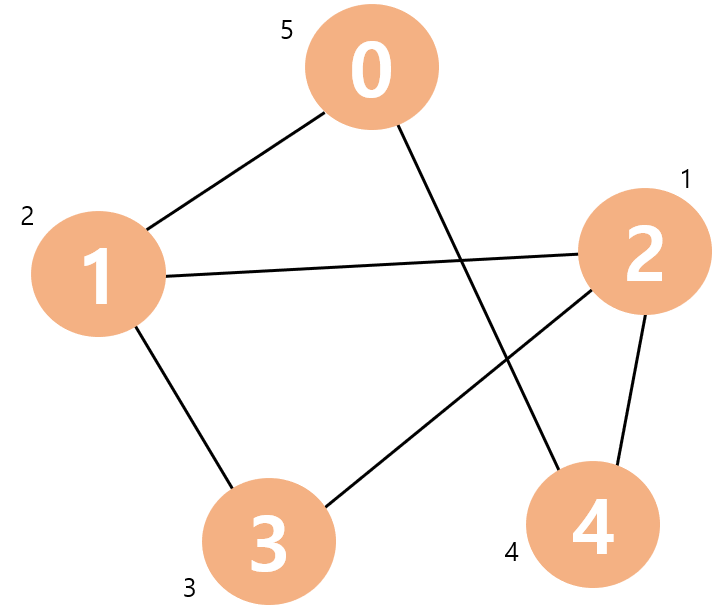
그래프에서 하나의 노드로부터 각 노드까지의 최단 거리를 구하기 위한 알고리즘으로,

코딩 테스트의 경로 탐색 문제를 해결하기 위해 기본적으로 알아야 한다.

다익스트라와 달리 모든 노드 쌍에 관한 최단 거리를 구하는 '플로이드-워셜 알고리즘'이 있다.

(다익스트라를 각 노드에 대해 구하면 동일하게 모든 쌍에 관한 최단 거리를 구할 수 있다.)

동작

 dist[i] = min( dist[i], dist[j] + wieght[j][i] )

(i노드까지의 최단거리) = (현재 i 노드까지의 최단거리), (이전 노드 j까지의 최단거리 + j 에서 i까지 거리)

두 값중 작은 값을 취하면 된다. 위 공식을 시작 노드로부터 점진적으로 진행시키면 된다.

BFS와 같이 queue를 이용하여 다음 노드로 진행 시키는데, 우선 순위 큐(힙)을 사용하면

업데이트 횟수가 줄어들어 더 빠르게 진행할 수 있다. (여기서도 우선 순위 큐로 설명한다.)

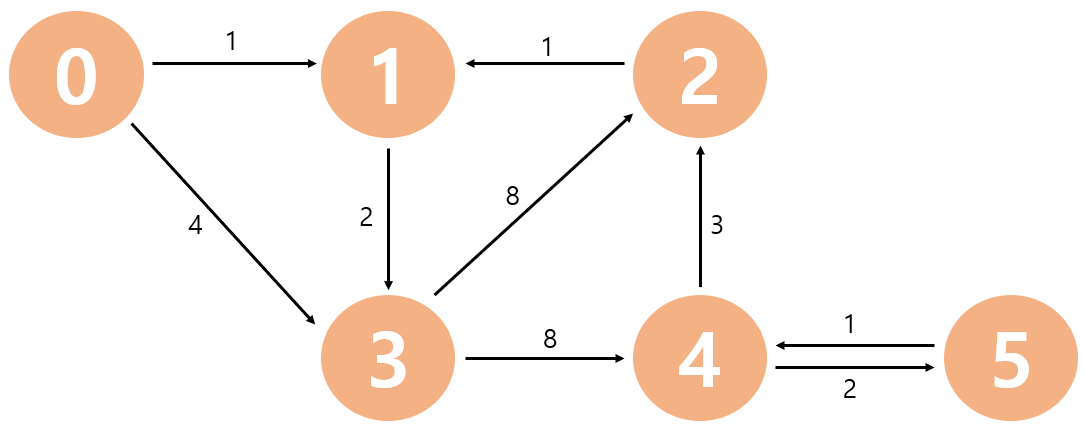
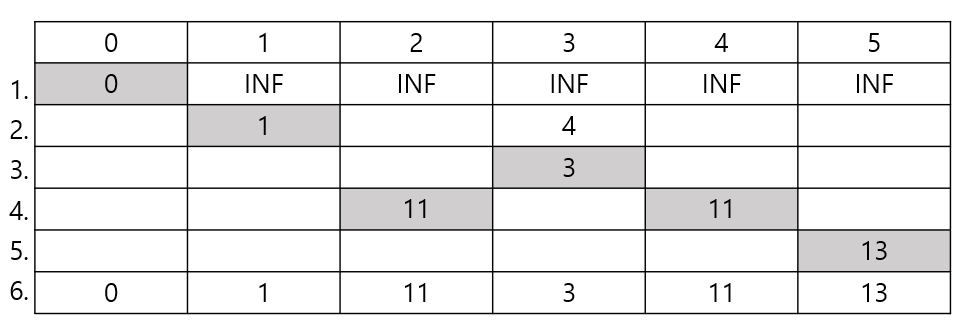
먼저 최단 거리를 저장한 배열을 선언하고 시작 노드(0번)에 거리(시작이므로 0)를 표시한 뒤,

나머지 노드에 INF(무한한값, 보통 -1로 둔다.)으로 채워 넣고, queue에 시작 노드를 넣는다.

    1. queue에서 데이터를 꺼내어(0번) 연결된 모든 노드(1, 3번)의 거리를 계산하고 기록한 뒤,

       기록된 거리값으로 queue에 삽입한다.

    2. queue에서 데이터를 꺼내어(최소힙이므로 1번) 연결된 모드 노드(3번)의 거리를 계산하여 더 작으므로

       업데이트 한다. 업데이트 되었으므로 다시 queue에 삽입한다.

    3. queue에서 데이터를 꺼내고(3번) 연결된 모든 노드(2, 4번)의 거리 계산 후 기록한 뒤, queue에 삽입한다.

       구현에 따라 다르지만, 현재 queue에 거리4로 먼저 넣은 3번 노드가 있지만 거리3으로 구한 것이 최단이므로,

       무시된다. 최소힙으로 구현하는 이점이다.

    4. queue에서 데이터를 꺼내어(2번) 연결된 모든 노드(1번)의 거리를 계산하지만 이미 1번에 더 작은 값이 있으므로,

       무시된다. 또 데이터를 꺼내어(4번) 연결된 모든 노드(5번)에 대해 계산하여 갱신 시킨다. 그 후 queue에 넣는다.

    5. queue에서 데이터를 꺼내어(5번) 연결된 모든 노드(4번)에 대해 계산하지만 이미 작은 값이 있어 무시된다.

       queue에 더이상 데이터가 없으므로 알고리즘을 종료한다.

    6. 시작 노드(0번)으로부터 각 노드까지의 최단 거리가 다 구해졌다.

코드

public class graph {
	// 최소힙에 넣기 위해 정의한 (노드번호, 거리)쌍의 클래스
	private class _pair implements Comparable<_pair> {
		public int dst;
		public int weight;
		public _pair(int d, int w) {
			this.dst = d;
			this.weight = w;
		}

		// 비교를 위해 Override
		@Override
		public int compareTo(_pair target) {
			return this.weight <= target.weight ? -1 : 1;
		}
	}
    
	private ArrayList<_pair>[] adjList; // 인접 리스트
	private PriorityQueue<_pair> queue; // 우선 순위 큐
	private int[] shortestDist;         // 최단 거리 배열
	
	public graph(int n) {
		adjList = new ArrayList[n];
		shortestDist = new int[n];
		
		Arrays.fill(shortestDist, -1);
		for (int i = 0; i < n; i++) {
			adjList[i] = new ArrayList();
		}
		queue = new PriorityQueue<>();
	}
	
	// 간선 추가
	public void addEdge(int src, int dst, int w) {
		this.adjList[src].add(new _pair(dst, w));
	}
	
	// 다익스트라
	public void dijkstra(int start) {
		// 시작 노드 삽입, 거리 행렬 기록
		queue.offer(new _pair(start, 0));
		shortestDist[start] = 0;
		
		// 큐에 데이터가 없을 때까지
		while (!queue.isEmpty()) {
			_pair p = queue.poll();
			
			for (_pair adj : adjList[p.dst]) {
				int dist = adj.weight + p.weight;
				
				// 계산된 거리가 기록되어있는 거리보다 작거나
				// INF값( -1 )일 경우
				if (dist < shortestDist[adj.dst] || shortestDist[adj.dst] == -1) {
					shortestDist[adj.dst] = dist;
					
					queue.offer(new _pair(adj.dst, dist));
				}
			}
		}
	}
	
	// 최단 거리 배열 출력
	public void printDist() {
		for (int i : shortestDist) {
			System.out.print(i + " ");
		}
		System.out.println();
	}
}

public class Main {

	public static void main(String[] args) {
		graph g = new graph(6);
		
		g.addEdge(0, 1, 1);
		g.addEdge(0, 3, 4);
		g.addEdge(1, 3, 2);
		g.addEdge(2, 1, 1);
		g.addEdge(3, 2, 8);
		g.addEdge(3, 4, 8);
		g.addEdge(4, 2, 3);
		g.addEdge(4, 5, 2);
		g.addEdge(5, 4, 1);
		
		g.dijkstra(0);
		
		g.printDist();
	}
}

BFS

DFS는 연결된 노드 하나를 먼저 방문하는 것에 비해 BFS의 경우 연결된 노드 전체를 먼저 방문하는 것이 우선이 된다.

동작을 간단하게 보면 다음과 같다.

( 그래프는 DFS때와 동일한 무방향 그래프를 사용한다.)

2번 노드 부터 시작하면 먼저 큐에 2를 푸쉬해 둔다.

  1. poll하여 큐 최하단 노드를 꺼내어 방문 표시를 하고 출력한다.

  2. 해당 노드의 인접 노드중 미방문 노드를 전부 push한다.

  2. 큐가 빌때까지 1, 2번을 계속한다.

예시 그래프의 노드를 위 순서대로 진행하면 2 1 3 4 0가 된다.

코드

저번 dfs코드를 재귀호출이 아닌 스택을 직접적으로 사용할 경우 중복 제거를 했어야 함에 반해,

bfs의 특성상 중복 제거를 하지 않아도 결과는 동일하다.

import java.util.*;

public class graph {
	private int szVertex;
	private ArrayList<Integer> adjList[];
	private boolean visited[];
	private Queue<Integer> queue;				// for BFS
	
	public graph(int v) {
		szVertex = v;
		visited = new boolean[szVertex];		// default false
		adjList = new ArrayList[szVertex];
		for (int i = 0; i < szVertex; i++) {
			adjList[i] = new ArrayList();
		}
		queue = new LinkedList<Integer>();
	}
	
	public void addEdge(int from, int to) {
		// 무방향 그래프이므로 반대의 경우도 추가
		adjList[from].add(to);
		adjList[to].add(from);
	}
	
	// 재귀 호출로 구현할 수 있지만 queue을 이용하여 구현하였다
	public void BFS(int start) {
		queue.add(start);
		
		// queue가 비어질때까지 게속
		while (queue.peek() != null) {
			// queue에서 가장 오래전 삽입된 데이터를 꺼내어 방문 행렬에 표시하고 출력
			int current = queue.poll();
			
			// 미방문 정점의 경우
			if (!visited[current]) {
				visited[current] = true;
				System.out.print(current + " ");
				
				// 인접 리스트에서 미방문 정점의 경우 queue에 추가
				for (int i : adjList[current])
					if (!visited[i])
						queue.add(i);
			}
		}
		System.out.println();
	}
	
	// 첫노드가 주어지지 않을 경우 0번 부터
	public void BFS() {
		BFS(0);
	}
}

public class bfs {

	public static void main(String[] args) {
		graph g = new graph(5);
		
		g.addEdge(0, 1);
		g.addEdge(0, 4);
		g.addEdge(1, 2);
		g.addEdge(1, 3);
		g.addEdge(2, 3);
		g.addEdge(2, 4);
		
		g.BFS(2);
	}
}

 DFS는 그래프나 트리에서 탐색하는 대표적인 두가지 방법(DFS, BFS)중 하나로, 하위 혹은 연결된 노드 중 하나를

우선적으로 방문하는 형태이다. 여기에서는 무방향 그래프를 사용하여 알아 보도록 한다.

인접 행렬, 인접 리스트

 먼저 그래프의 구현에 앞서 인접 행렬과 인접 리스트가 있다.

인접 행렬의 경우 NxN의 행렬로(N은 노드 개수)로 표시하는 것으로, 다음과 같이 표시한다.

0, 1의 노드가 연결되어 있는 경우, adjArray[0][1] = 1로 표시한다.

무방향 그래프의 경우 인접 행렬의 대각선(푸른선)을 기준으로 뒤집어진 대칭을 이루고 있다.

현재 행렬값이 모두 1로 되어 있지만 가중치 그래프의 경우 행렬의 숫자를 바꾸면 된다.

장점 : 

    구현이 비교적 간단하다.

    i, j노드의 연결을 확인할 경우 adjArray[i][j]로 바로 확인할 수 있어, O(1)의 시간복잡도를 가진다.

단점 :

    i 노드에 연결된 모든 노드를 확인하고자 할때 adjArray[i][0] ~ adjArray[i][N-1] 모두 확인해야해서

    O(N)의 시간복잡도를 가진다. 노드가 많고 간선(연결)이 적을때 비효율이다.

    공간복잡도도 O(N^2)로 메모리를 많이 차지한다.

 인접 리스트의 경우 연결된 노드들의 리스트로 다음과 같이 표현한다.

0, 1의 연결을 확인하고 싶은 경우 adjList[0] 리스트를 순회하여 1번이 있는 지 확인하면 된다.

무방향의 경우 인접 행렬과 동일하게 0, 1이 연결된다면 1, 0의 연결도 추가하여야 한다.

장점 :

    i와 연결된 모든 노드를 확인하고자 할때 최악의 경우(i가 모든 노드와 연결된 경우) O(N)이지만,

    대부분의 경우 항상 O(N)인 인접행렬보다 빠르다.

    공간복잡도도 간선의 개수를 E라 할때 최악의 경우를 제외하고 O(E) < O(N^2)이므로 낭비가 적다.

단점 :

    i, j의 연결을 확인하고 싶을때 adjList[i]를 순회하며 j가 있는지 봐야 하므로 O(N)으로 인접행렬보다 느리다.

DFS

dfs의 동작을 간단하게 보면 다음과 같다.

2번 노드 부터 시작하면 먼저 스택에 2를 푸쉬해 둔다.

  1. pop하여 스택 최상단 노드를 꺼내어 방문 표시를 하고 출력한다.

  2. 해당 노드의 인접 노드중 미방문 노드를 전부 push한다. 이때 스택에 중복 push는 없게 한다.

  2. 스택이 빌때까지 1, 2번을 계속한다.

예시 그래프의 노드를 위 순서대로 진행하면 2 1 0 3 4가 된다.

코드

함수 호출이 스택메모리를 사용하므로 재귀호출로도 구현할 수 있다.

이번 코드에서는 JAVA에서 지원하는 stack 컨테이너로 구현하였다.

스택에 중복 데이터에 대한 예외처리를 하지 않았기 때문에 탐색 순서가 다르게 나올 수 있다.

(스택에 들어있는지 확인하는 행렬 같은 거를 추가하면 쉽게 구현할 수 있다.)

import java.util.*;

public class graph {
	private int szVertex;
	private ArrayList<Integer> adjList[];
	private boolean visited[];
	private Stack<Integer> stack;				// for DFS
	
	public graph(int v) {
		szVertex = v;
		visited = new boolean[szVertex];		// default false
		adjList = new ArrayList[szVertex];
		for (int i = 0; i < szVertex; i++) {
			adjList[i] = new ArrayList();
		}
		stack = new Stack();
	}
	
	public void addEdge(int from, int to) {
		// 무방향 그래프이므로 반대의 경우도 추가
		adjList[from].add(to);
		adjList[to].add(from);
	}
	
	// 재귀 호출로 구현할 수 있지만 stack을 이용하여 구현하였다
	public void DFS(int start) {
		stack.push(start);
		
		// stack이 비어질때까지 게속
		while (!stack.isEmpty()) {
			// stack 최상단을 꺼내어 방문 행렬에 표시하고 출력
			int current = stack.pop();
			
			// 미방문 정점의 경우
			if (!visited[current]) {
				visited[current] = true;
				System.out.print(current + " ");
				
				// 인접 리스트에서 미방문 정점의 경우 스택에 추가
				for (int i : adjList[current])
					if (!visited[i])
						stack.push(i);
			}
		}
		System.out.println();
	}
	
	// 첫노드가 주어지지 않을 경우 0번 부터
	public void DFS() {
		DFS(0);
	}
}

public class dfs {

	public static void main(String[] args) {
		graph g = new graph(5);
		
		g.addEdge(0, 4);
		g.addEdge(1, 3);
		g.addEdge(2, 4);
		g.addEdge(2, 3);
		g.addEdge(1, 2);
		g.addEdge(1, 0);
		
		g.DFS(2);
	}
}

local outlier fator(이하 lof)는 각 점들의 밀도와 이웃점들의 밀도를 고려하여 해당 점의 스코어를 계산합니다.

lof를 구하기 앞서 먼저 reachability-distance를 구해야 한다.

reachability-distance(A,B)는  두 점 사이의 거리와 B에서 k번째 근접이웃까지의 거리중

큰 값이 reachability-distance의 값이 된다. 예를 들어,

위 그림에서 빨간선으로 이어진 점들을 B라고 볼때,

A까지의 거리가 각 점들에서 k-distance보다 크므로 빨간선이 reachability-distance값이 된다.

그 다음으로 lrd(local reachability density)를 구해야 한다.

여기서 Nk는 k-distance내 점들의 집합이다.

A가 밀도가 높지 않은 지역에 위치할 경우 A로부터 집합내의 점 B까지 거리가 길어지므로,

A의 lrd값은 작아진다.

최종적으로 lof는 주변 이웃 점들의 평균 lrd값을 구하고,

A의 lrd값을 나누어줌으로써 구해진다.

위에서 언급했듯,

A가 밀도가 높지 않은 지역에 위치할 경우 lrd값은 작아지므로 반대로 lof값은 커진다. (분모이므로)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor

print(__doc__)

np.random.seed(42)

# Generate train data
X_inliers = 0.3 * np.random.randn(100, 2)
X_inliers = np.r_[X_inliers + 2, X_inliers - 2]

# Generate some outliers
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
X = np.r_[X_inliers, X_outliers]

n_outliers = len(X_outliers)
ground_truth = np.ones(len(X), dtype=int)
ground_truth[-n_outliers:] = -1

# fit the model for outlier detection (default)
clf = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
# use fit_predict to compute the predicted labels of the training samples
# (when LOF is used for outlier detection, the estimator has no predict,
# decision_function and score_samples methods).
y_pred = clf.fit_predict(X)
X_scores = clf.negative_outlier_factor_

plt.title("Local Outlier Factor (LOF)")
plt.scatter(X[:, 0], X[:, 1], color='k', s=3., label='Data points')
# plot circles with radius proportional to the outlier scores
radius = (X_scores.max() - X_scores) / (X_scores.max() - X_scores.min())
plt.scatter(X[:, 0], X[:, 1], s=1000 * radius, edgecolors='r',
            facecolors='none', label='Outlier scores')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
n=np.copy(X_scores*-1) # 스코어값이 음수로 나오므로
n[n<2]=np.nan          # 스코어값이 2보다 작으면 표시 안함
n=np.round(n,2)
for i, txt in enumerate(n):
    if np.isnan(txt):continue
    plt.annotate(txt, (X[i,0], X[i,1]))
legend = plt.legend(loc='upper left')  # 범례 위치
plt.show()

-----------------------------------------------------------------------------------------------------------------------------------

참고

https://scikit-learn.org/stable/auto_examples/neighbors/plot_lof_outlier_detection.html

https://jayhey.github.io/novelty%20detection/2017/11/10/Novelty_detection_LOF/

https://godongyoung.github.io/머신러닝/2019/03/11/Local-Outlier-Factor(LOF).html

ball tree도 kd tree와 마찬가지로 knn(k-nearest neighbor) search에 많이 쓰이는 트리이다.

kd tree보다는 초기 트리 구성에 비용이 크지만, kd tree의 경우 차수가 아주 크면

query했을때 검색이 매우 느려지는데, ball tree는 kd tree보다 훨씬 빠르게 결과를 도출한다.

a(1,1550), b(900,440), c(2500,330), d(4000,2), e(5000,1)

위와 같은 데이터가 주어졌을때의 트리의 구성은 그림과 같다.

먼저 가장 범위가 큰 차수로 정렬을 시키고 (위 데이터에서는 1번째 차원의 범위가 1~5000이므로 가장 크다)

중간값을 취하고 왼쪽, 오른쪽으로 나눈 뒤 다시 재귀적으로 트리를 구성하도록 한다.

검색에 활용하도록 반지름 값도 구하는데 자식 노드중 가장 멀리 떨어진 노드와의 거리가 반지름이 된다.

이때, leaf size가 1보다 큰 경우 중간값을 size만큼의 개수를 취한다.

(leaf size는 검색 결과에 영향은 없지만 검색 속도에 영향이 있을 수 있다.)

예시 데이터를 기반으로 'ball'을 그려보면 다음과 같을 것이다.

알고리즘 설명및 코드의 한글 자료는 거의 전무하여 (내 검색 능력이 모자른 것일 수도)

위키백과와 사이트의 내용을 참고하였다.

import numpy as np

class Node:
    def __init__(self, data, radius, depth, left_child=None, right_child=None):
        self.left_child = left_child
        self.right_child = right_child
        self.data = data
        self.radius = radius
        self.depth = depth

    def printALL(self):
        print(self.radius, self.data, self.depth)
        if self.left_child != None:
            self.left_child.printALL()
        if self.right_child != None:
            self.right_child.printALL()

def balltree(ndata, depth):
    if ndata.shape[0] < 1:
        return None

    # element가 한 개일 경우
    if ndata.shape[0] == 1:
        return Node(
            data=np.max(ndata, 0).tolist(),
            radius=0,
            depth=depth,
            left_child=None,
            right_child=None
        )
    else:
        # 범위가 가장 큰 dimension에 따라 정렬
        largest_dim = np.argmax(ndata.max(0) - ndata.min(0))
        i_sort = np.argsort(ndata[:, largest_dim])
        ndata[:] = ndata[i_sort, :]

        nHalf = int(ndata.shape[0] / 2)
        loc = ndata[nHalf, :]
        data = loc.tolist()

        # 중간 값(data)에서 가장 멀리 떨어진 값 까지의 거리
        radius = np.sqrt(np.max(np.sum((ndata - loc) ** 2, 1)))

        return Node(
            data=data,
            radius=radius,
            depth=depth,
            left_child=balltree(ndata[:nHalf], depth+1),
            right_child=balltree(ndata[nHalf+1:], depth+1)
        )

if __name__ == '__main__':
    X = [[1,1550], [900,440], [2500,330], [4000,2], [5000,1]]
    X = np.asarray(X)

    tree = balltree(X, 0)
    tree.printALL()

역시 파이썬 패키지중 sklearn에서 balltree의 생성 및 검색을 간편하게 할 수 있다.

결과로 가장 유사한 데이터의 인덱스 번호와 거리를 반환한다.

import numpy as np
from sklearn.neighbors import BallTree

X = [[1,1550], [900,440], [2500,330], [4000,2], [5000,1]]
X = np.asarray(X)

# 트리 생성
tree = BallTree(X)

# 테스트 데이터 쿼리
dist, ind = tree.query([[1, 1551]], 1)

print(dist, ind)

-----------------------------------------------------------------------------------------------------------------------------------

참고

https://en.wikipedia.org/wiki/Ball_tree

https://www.astroml.org/book_figures/chapter2/fig_balltree_example.html

kd 트리는 이진 트리로, 모든 트리의 노드가 k차원으로 이루어져 있다.

최근 30차원의 데이터를 다루며 검색 및 존재 하지 않을 경우 유사도(유클리디안 거리)를 구하기 위해

보게 되었는데, 아쉽게도 트리를 구성하는 데이터가 10만개가 넘다보니 오래 걸렸다. (내 컴퓨터가 구린 것일 수도...)

어쨌든 간단하게 살펴보면,

a(7,2), b(5,4), c(9,6), d(4,7), e(8,1) 이 순으로 데이터가 트리가 삽입된다 하자

먼저 k=2가 된다.

a는 트리가 비어 있으므로 루트노드가 된다.

a의 x좌표를 비교하여 작은 애들은 왼쪽으로 큰 애들은 오른쪽으로 분류한다.

따라서 b는 a의 왼쪽 노드, c는 오른쪽 노드가 된다.

d의 x좌표는 a의 x좌표보다 작으므로 왼쪽으로 가지만 이미 b가 있으므로 이번에는 y좌표를 비교한다.

b의 y좌표보다 d의 y좌표가 크므로 오른쪽에 위치한다. 동일하게 e도 배치하면 위 그림과 같이 트리가 구성된다.

데이터 순서에 따라 트리의 구성이 달라지고 그에 따라 검색 속도도 천차만별로 바뀌게 된다.

이것을 막고자 트리 구성시 정렬 후 중간값을 취하도록 하는 방법도 있다.

from operator import itemgetter

class Node:
    def __init__(self, data, depth, left_child=None, right_child=None):
        self.left_child = left_child
        self.right_child = right_child
        self.data = data
        self.depth = depth
    def printALL(self):
        print(self.depth, self.data)
        if self.left_child != None:
            self.left_child.printALL()
        if self.right_child != None:
            self.right_child.printALL()


def kdtree(point_list, depth=0):
    if not point_list:
        return None

    k = len(point_list[0])
    axis = depth % k

    point_list.sort(key=itemgetter(axis))
    median = len(point_list) // 2

    return Node(
        data=point_list[median],
        depth=depth,
        left_child=kdtree(point_list[:median], depth + 1),
        right_child=kdtree(point_list[median + 1:], depth + 1)
    )

if __name__ == '__main__':
    point_list = [(7, 2), (5, 4), (9, 6), (4, 7), (8, 1), (2, 3)]
    tree = kdtree(point_list)
    tree.printALL()

위 코드는 위키백과의 것을 알기 쉽게 수정한 것이다.

트리 구성시 정렬하여 중간값을 취하고 재귀적으로 왼쪽과 오른쪽을 구하고 있다.

또한 python의 scipy라이브러리내 kdtree의 생성과 검색을 제공하고 있다.

from scipy import spatial

if __name__ == '__main__':
    point_list = [(7, 2), (5, 4), (9, 6), (4, 7), (8, 1), (2, 3)]
    tree = spatial.KDTree(point_list)

    print(tree.query((2, 3)))
    print(tree.query((2, 3.5)))

트리의 인자값으로 넣을 컨테이너로써 튜플이나 리스트외에도

DataFrame과 ndarray도 넣을 수 있다. query메소드로 검색하면 결과로

유클리디안 거리와 가장 유사한 노드의 인덱스 번호를 반환한다.

"""
 keras를 이용한 x1*100 + x2*200 + 150 학습 모델
"""
from tensorflow import keras

import numpy as np
from random import randint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 학습데이터 생성
x = [ randint(0, 100) for i in range(100000) ]
y = [ x[i*2]*100 + x[i*2+1]*200 + 150 for i in range(50000) ]
x = np.asarray(x).astype(np.float32)
x = x.reshape((50000, 2))
y = np.asarray(y).astype(np.float32)
y = y.reshape((50000, 1))

"""
# 학습 데이터 그래프 그리기
xs = x[:,0]
ys = x[:,1]
zs = y

fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(xs, ys, zs)
ax.view_init(15, 15)
plt.show()
"""

# 검증 데이터 생성
test_x = [ randint(0, 100) for i in range(100) ]
test_y = [ test_x[i*2]*100 + test_x[i*2+1]*200 + 150 for i in range(50) ]
test_x = np.asarray(test_x).astype(np.float32)
test_x = test_x.reshape((50, 2))
test_y = np.asarray(test_y).astype(np.float32)
test_y = test_y.reshape((50, 1))

# 모델 생성
model = keras.Sequential()
model.add(keras.layers.Dense(1, input_shape=(2,)))
rmsprop = keras.optimizers.RMSprop(lr=0.02)
model.compile(loss='mean_squared_error', optimizer=rmsprop, metrics=[keras.metrics.mse])
model.summary()

# 학습
model.fit(x, y, epochs=10)

# 검증 데이터로 모델 평가 (verbose = 1 출력 모드)
model.evaluate(test_x, test_y, verbose=1)

ret = model.predict(test_x[:3])
print("예측 데이터 : ", ret)
print("실제 데이터 : ", test_y[:3])

tensorflow에 keras가 들어오면서 훨씬 더 간단하게 모델을 만들고 돌려볼 수 있게 되었다.

Representation

뉴럴 네트워크는 딥러닝의 토대가 되는 기술로 동물의 뇌의 뉴런의 행위를 모방한 알고리즘이다.

위 사진은 뉴런을 도식화 한 것인데 Dendrite는 외부로부터의 전기신호를 받는 "input wires"이고

Axon은 Nuclues에서 가공이 된 신호를 외부로 보내는 "output wire"가 된다. 이는 매우 함수의 형태와 비슷한데

기존의 2진 로지스틱에 빗대어 보면 왼쪽 그림처럼 표현할 수 있겠다.

(타 강의나 프레임워크에서의 표현과 달리 앤드류응교수님의 강의는

'x0 = 1'인 열을 추가해서 'X*∂+b'가 아니라 'X*∂'인 것이

가끔 헷갈리네요 ㅠㅠ 멍청한가 봅니다.)

단일 뉴런의 형태를 위와 같이 표현하면 뉴럴 네트워크란 여러 뉴런이 연결되어있는 것처럼

위의 형태를 다수 연결하여 그룹이 된 것이다.

왼쪽 그림처럼 input으로 x1, x2, x3이 있고 각 뉴런 a1, a2, a3에 넣어주고 있다.

그리고 그 결과를 다시 마지막 뉴런에 보낸다.

이것이 뉴럴 네트워크인 것인다.

(뉴럴 네트워크에서 Layer1은 input layer,

마지막 Layer3은 output layer라 부르며

그 사이의 모든 layer는 hidden layer라고 부른다. 단일 뉴런(로지스틱)에서 처럼

학습셋업시 input의 X벡터와 output의 h(x)의 결과와 y값과의 차이 외에는

보지 않기 때문이다.)

위 뉴럴 네트워크의 hypothesis를 표현하면 이렇게 된다.

여기서 g는 로지스틱 함수이며 bias값을 위한 x0를 포함한 X벡터가 각 Layer2의 뉴런들에 들어가서 그 결과인

a1, a2, a3가 다시 최종 레이어의 input으로 들어가는 형태이다. (물론 bias를 위해 a0가 추가된다.)

이걸 벡터화 해서 표현하면

이렇게 될 것이다.

더 간단히 수식으로 표현하면:

z(j+1)=Θ(j)a(j)

hΘ​(x)=a(j+1)=g(z(j+1))

이 된다.

XOR 문제

xor 문제(혹은 xnor)문제는 선형적으로는 풀 수 없다.

xor를 뉴럴네트워크(이하 NN)가 해결할 수 있으면

오른쪽 그래프와 같은 복잡한 문제도 해결 할 수 있을 것이다.

다른 논리 연산들은 대부분 선형적으로(단일 뉴런) 풀 수 있다.

대표적으로 AND를 예로 들면

∂0 = -20, ∂1 = +20, ∂0 = +20이라 가정할때 오른쪽 표와 같은 결과를

얻을 수 있을 것이다. 

OR나 NOT등의 논리 연산 또한 선형적으로 구할 수 있으며

결록적으로 XNOR은 이러한 논리연산들을 연결하여 구할 수 있다.

진리표로 예를 들자면

(편의상 c언어의 비트연산자로 표현)

쉽게 알 수 있다. 이처럼 각 논리연산을 하는 뉴런을 연결하면 아래와 같이 될 것이다.

이로 인해 XNOR문제는 NN을 이용해 풀 수 있는 것을 보았다.

마찬가지로 XOR 또한 NOT레이어를 더 추가하든, 최종 결과값을 뒤집든 해서 동일하게 구할 수 있음을 알 수 있다.

과정은 인증서를 설정해주는 것 외에는 보통의 hHttpURLConnection을 이요한 통신과 흡사하다.

private HttpsURLConnection urlConnection;
    private String method;
    private SSLContext sslContext;

    public static int BUFFER_SIZE = 1024;

    public HttpsURLConnection getConnection(Context context, String url, String requestMethod) {
        try {
            setCertification(context);

            // URL 설정
            URL request_url = new URL(url);
            method = requestMethod;

            urlConnection = (HttpsURLConnection) request_url.openConnection();
            urlConnection.setRequestMethod(method);
            urlConnection.setReadTimeout(95 * 1000);
            urlConnection.setConnectTimeout(95 * 1000);
            urlConnection.setDoInput(true);

            if (requestMethod.equals("GET"))
            {
                urlConnection.setRequestProperty("Accept", "application/json");
                urlConnection.setRequestProperty("X-Environment", "android");
            } else {
                urlConnection.setRequestProperty("Content-Type", "application/json; charset=UTF-8");
                urlConnection.setRequestProperty("X-Environment", "android");
            }

            urlConnection.setHostnameVerifier(new HostnameVerifier() {
                @Override
                public boolean verify(String hostname, SSLSession session) {
                    return true;
                }
            });
            // 위에서 설정한 인증서 사용
            urlConnection.setSSLSocketFactory(sslContext.getSocketFactory());

            urlConnection.connect();

        } catch(ConnectException ce) {
            // 커넥션 오류
            ce.printStackTrace();
            return null;
        } catch (Exception e) {
            e.printStackTrace();
        }

        return urlConnection;
    }

주의점은 HttpURLConnection이 아닌 HttpsURLConnection이다. 's'가 붙어있다.

메소드는 HttpURLConnection을 상속하고 있어서 비슷하다.

    private void setCertification(Context context) throws Exception {
        CertificateFactory cf = CertificateFactory.getInstance("X.509");

        InputStream caInput = context.getResources().openRawResource(R.raw.nive_crt);
        Certificate ca;
        try {
            ca = cf.generateCertificate(caInput);
            System.out.println("ca=" + ((X509Certificate) ca).getSubjectDN());
        } finally {
            caInput.close();
        }

        // Create a KeyStore containing our trusted CAs
        String keyStoreType = KeyStore.getDefaultType();
        KeyStore keyStore = KeyStore.getInstance(keyStoreType);
        keyStore.load(null, null);
        keyStore.setCertificateEntry("ca", ca);

        // Create a TrustManager that trusts the CAs in our KeyStore
        String tmfAlgorithm = TrustManagerFactory.getDefaultAlgorithm();
        TrustManagerFactory tmf = TrustManagerFactory.getInstance(tmfAlgorithm);
        tmf.init(keyStore);

        // Create an SSLContext that uses our TrustManager
        sslContext = SSLContext.getInstance("TLS");
        sslContext.init(null, tmf.getTrustManagers(), null);
    }

코드 원본 : https://developer.android.com/training/articles/security-ssl?hl=ko

구글 문서에서 제공하는 코드이다. 인증서 데이터는 /res/raw/ 에 두고 openRawResource()메소드로 가져오고 있다.

    public String request(String content) {
        try {
            if(method.equals("POST")) {
                // POST 일때만 실행
                OutputStream outputStream = urlConnection.getOutputStream();
                BufferedWriter bufferedWriter = new BufferedWriter(new OutputStreamWriter(outputStream, "UTF-8"));
                bufferedWriter.write(content);
                bufferedWriter.flush();
                bufferedWriter.close();
                outputStream.close();
            }

            String response = null;
            if (urlConnection.getResponseCode() == HttpURLConnection.HTTP_OK) {
                response = readStream();
            }

            urlConnection.disconnect();

            return response;
        }
        catch (Exception ex) {
            ex.printStackTrace();
        }

        return null;
    }

    private String readStream() throws Exception {
        StringBuilder responseStringBuilder = new StringBuilder();

        BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(urlConnection.getInputStream()));
        for (; ; ) {
            String stringLine = bufferedReader.readLine();
            if (stringLine == null) break;
            responseStringBuilder.append(stringLine + '\n');
        }
        bufferedReader.close();

        return responseStringBuilder.toString();
    }

    public void disconnect() {
        urlConnection.disconnect();
    }

요청, 응답 코드

SHA는 Secure Hash Algorithm의 줄임말로 1993년 미국 국가안보국(NSA)에 의해 설계되고 표준으로 지정되었다.

이때 출간된 SHA는 구분상 SHA-0이라하고 2년 뒤인 1995년에 개정된 SHA-1을 발표했고 현재 널리 쓰이는 해쉬 알고리즘이다.

이후 변형 버전인 SHA-2라 불리는 SHA-224, 256, 384, 512가 나왔으며 보통은 SHA-1을 사용하고 더 암호학적 안전을 요하는 곳에는

SHA-2를 사용한다.

SHA-1은 메시지 길이에 상관없이 512비트씩 잘라서 메시지 다이제스트 함수를 돌린 뒤 160비트의 출력을 낸다.

원본 메시지 + 패딩 + 원본 메시지 길이(64비트) 가 512비트의 배수가 되도록 만든다. (메시지가 없어도 한다.)

패딩은 맨 뒤 64비트에는 메시지 전체 길이를 넣고 나머지 비트는 최상위 비트 1을 제외하고 0으로 채운다.

메시지가 512비트보다 길 경우 다음 번 메시지 다이제스트 함수의 입력으로 전 함수의 출력을 받는다.

맨 앞 초기값 ABCDE는 정해진 상수값이다.

void SHA_1(FILE* fptr, BYTE* result) {
	int i, size = 0;

	BYTE msg[HASH_BLOCK * 2] = { 0, };
	UINT64 f_size = 0;

	SHA_1_init();

	while ((size = fread(msg, sizeof(BYTE), HASH_BLOCK, fptr))) {
		f_size += size;

		if (size < HASH_BLOCK)
			padding(msg, f_size);

		SHA_1_digest(msg);
		if (isAddpad) SHA_1_digest(msg + HASH_BLOCK);
		memset(msg, 0, HASH_BLOCK * 2);
	}

	for (i = 0; i < HASH_DATA; i++)
		result[i] = digest[i];
}

void padding(BYTE* in, UINT64 msg_len)
{
	int i;
	BYTE* ptr = (BYTE*)&msg_len;

	in[msg_len % HASH_BLOCK] = 0x80;
	msg_len *= 8;

	// 메시지가 448비트 보다 작은 경우와 448비트 보다 큰 경우로 나누어 처리
	// 448비트보다 큰 경우에는 512비트의 블록을 추가하여 패딩을 수행한다
	if ((msg_len % HASH_BLOCK) < 56)
	{
		for (i = 0; i<8; i++)
			in[HASH_BLOCK - i - 1] = *(ptr + i);
	}
	else
	{
		isAddpad = 1;
		for (i = 0; i<8; i++)
			in[HASH_BLOCK * 2 - i - 1] = *(ptr + i);
	}
}

파일을 읽고 크기가 64바이트(512비트)보다 작으면 패딩을 한다. 패딩에서 메시지가 448비트보다 커서 문자열 길이를 담을 수 없는 경우

블록을 하나 더 늘리고 메시지 다이제스트 함수도 한번 더 한다.

메시지 다이제스트 함수는 총 80라운드를 돌며 초기 입력 160비트와 마지막 80번째 라운드의 출력 160비트를 32비트씩 법 2^32상에서의 덧셈을 한다.

그 값이 메시지 다이제스트 함수의 최종 출력값이 된다.

각 라운드는 위 그림과 같이 구성되는데 32비트씩 나누어 A->B', B->C', C->D', D->E'로 간단한데 (B->C'일때 좌측 순환쉬프트 30비트를 해준다.)

E->A'로 할때에는 A의 좌측 순환쉬프트를 5비트해준 값과 B,C,D를 F함수에 넣은 출력값과 E값과 Wt와 라운드 상수 Kt를 법 2^32상에서 덧셈을 하여

구한다. F함수는 오른쪽 그림과 같으며 F2와 F4는 같은 동작을 한다.

Wt는 입력블록을 32비트씩 잘라 16개의 W0~W15를 만들고 이를 이용하여 W79까지 생성할 수 있다.

void SHA_1_digest(BYTE* in) {
	int i;
	UINT M[16] = { 0, };
	UINT W[80] = { 0, };
	UINT reg[5] = { 0, };
	UINT temp;

	reg[0] = init_reg[0];
	reg[1] = init_reg[1];
	reg[2] = init_reg[2];
	reg[3] = init_reg[3];
	reg[4] = init_reg[4];

	for (i = 0; i < 64; i += 4) {
		M[i / 4] = BTOW(in[i], in[i + 1], in[i + 2], in[i + 3]);
	}

	for (i = 0; i < 80; i++) {
		if (i < 16)
			W[i] = M[i];
		else
			W[i] = CIR_SHIFT((W[i - 16] ^ W[i - 14] ^ W[i - 8] ^ W[i - 3]), 1);
	}

	for (i = 0; i < 80; i++) {

		if (i < 20) {
			temp = CIR_SHIFT(reg[0], 5) + F1(reg[1], reg[2], reg[3]) + reg[4] + W[i] + K0;
		}
		else if (i < 40) {
			temp = CIR_SHIFT(reg[0], 5) + F2(reg[1], reg[2], reg[3]) + reg[4] + W[i] + K1;
		}
		else if (i < 60) {
			temp = CIR_SHIFT(reg[0], 5) + F3(reg[1], reg[2], reg[3]) + reg[4] + W[i] + K2;
		}
		else {
			temp = CIR_SHIFT(reg[0], 5) + F2(reg[1], reg[2], reg[3]) + reg[4] + W[i] + K3;
		}

		reg[4] = reg[3];
		reg[3] = reg[2];
		reg[2] = CIR_SHIFT(reg[1], 30);
		reg[1] = reg[0];
		reg[0] = temp;
	}

	init_reg[0] += reg[0];
	init_reg[1] += reg[1];
	init_reg[2] += reg[2];
	init_reg[3] += reg[3];
	init_reg[4] += reg[4];

	make_Bit160(init_reg[0], init_reg[1], init_reg[2], init_reg[3], init_reg[4]);
}