이번에는 선형 회귀 분석 알고리즘중 가장 간단한 Gradient Descent (경사 내려오기?)에 알아보자.
<그림 1>
위 그림 1처럼 현재 위치보다 작은곳으로 내려오는 알고리즘이다.
근데 위 곡면은 시작 위치에 따라 내려오는 지점이 다를 수 있다.
<그림 2-1>
그림 2-1의 내용이 Gradient descent 알고리즘의 과정이다.
" := " 은 대입연산자로써 프로그래밍 언어에서 " = "와 같다.
α는 learning rate로 얼마나 빨리 혹은 얼마나 느리게 내려올지를 정하는데 도움이 된다.
∂는 partial derivative(편미분) 기호이다.
수렴할때까지 진행하며 한번 수행시 모든 파라미터에대해(여기선 0~1) 수행한다.
<그림 2-2>
그림 2-1의 알고리즘 작성시 주의점은 그림 2-2의 오른쪽 처럼 하면은
세타0에 대입후 세타1에대해 계산시 세타0의 값이 달라져있기 때문에 바른값이 나오지 않으므로
주의해야 한다.
<그림 3-1>
그림 2-1의 알고리즘이 성립하는 이유를 살펴보자.
편의상 파라미터가 1개일때로 가정하자.
처음 세타값이 그림 3-1의 그래프처럼 최소점보다 오른쪽에 있을때
미분하면 양의 정수가 나올 것이다. 따라서
원래의 세타1에서 양수를 뺴므로 세타1은 작아진다.
작아지며 점점 최소점에 다가간다.
<그림 3-2>
반대로 세타값이 왼쪽에 있을때 미분하면 음수가 나온다.
음수를 빼면 더해지므로 세타값은 커진다.
커지며 점점 최소점에 다가간다.
<그림 4-1>
learning rate의 역할은 앞서 Gradient descent를 진행하며
빨리 내려올지 늦리게 내려올지를 결정한다고 하였다.
하지만 다른것도 그렇지만 항상 적당히가 중요하다.
learning rate값이 너무 작으면 그림4-1처럼 내려오는데 한참이 걸려
결과값을 얻는데 시간이 너무 오래 걸린다.
<그림 4-2>
반대로 너무 크면 그림 4-2처럼 내려오기는 커녕 오히려 위로 올라갈수도 있다.
그래서 적당량의 learning rate를 정해주는 것도 중요하다.
근데 learning rate를 계속 고정값으로 주어도 되는지 고민이 될 수도 있다.
최소점에 가까워질때마다 작게해주야할것같지만
다행히도 최소점에 가까워질수록 비용함수 J의 미분값이 0에 가까워지므로
세타의 증감량도 감소하므로 learning rate의 값을 변경하지 않아도 된다.
<그림 5>
위 그림 5에는 극소값이 2개가 있다.
그럼 만약 Gradient descent 진행 도중 그림 처럼 오른쪽 극소값을 만났을때 세타1의 증감은 어떻게 될까?
보시다시피 비용함수의 미분값이 0이 되므로 증감하지않고 멈추게 된다.
따라서 그림 1처럼 시작위치에 따라 얻는 결과가 다를 수 있는 문제가 있다.
<그림 6>
알고리즘에서 미분을 수행하여 그림 6의 아래처럼 식을 바꿀 수 있다.
Feature Scaling
<그림 7>
Gradient Descent시 결과값을 빠르게 취하기 위함이다.
변수들(크기, 화장실 수, 등등)의 범위를 대략 -1과 +1사이로 맞춘다.
위 수식 처럼 최대 크기로 나누어서 할 수 있으며
(avg는 해당 특성들의 평균)
이렇게도 할 수 있다. (현재 2번째 Scaling의 사용 이유를 잘 모르겠다. 아는 분은 코멘트좀 ㅠ)
Making sure gradient descent is working correctly
<그림 8>
그림 8처럼 gradient descent 반복 횟수에 따른 비용함수 크기가 증가하거나 일정구간을 반복될 경우
learning rate 값을 조금 줄일 필요가 있다.
Polynomial Regression
우리말로 다항 회귀 분석이라 한다.
<그림 9-1>
그림 9-1과 같은 그래프에서 최적의 직선을 구하여도
그래프의 점들이 직선보다는 곡선에 가깝게 분포하여 신뢰도가 떨어질 것이다.
그래서 polynomial regression은 최적의 곡선을 찾는다.
주로 2차나 3차곡선을 이용한다.
<그림 9-2>
그림 9-2의 2차곡선이 더 신뢰도가 있어보인다. 하지만 사이즈가 커지면 가격이
떨어질 수도 있다. (최대값 이후) 이 경우에는 밑의 9-3처럼 "루트"함수가 적합해 보인다.
<그림 9-3>
Normal Equation
<그림 10-1>
특성들이 있고 결과값이 있을때 행렬로 표현하면
이렇게 표현할 수 있다. (여기서 x0는 세타0과의 곱때문에 1로 둔다.)
결론 부터 위 방정식을 풀면 최적의 세타벡터를 얻을 수 있다.
식 도출) 위키백과

실제값과 hypothesis차이를 구하여
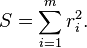
제곱의 합을 취하면 Cost Function과 같다. (앞서 보았던 cost function은 여기에 2m 나눔)
각 세타(여기 식에선 베타)에 대해 편미분하면

이고
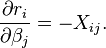
이므로 다시쓰면

이다. Cost Function값이 최저일때 미분하면 0이므로

이렇게 쓸 수 있다. 식을 정리하면

이므로 행렬로 표현하면

이되어 위 식을 구할 수 있다.
normal equation으로 반복작업 없이 바로 세타벡터를 구할 수 있지만 단점이 있다.
Gradient Descent와 비교하면
<그림 11>
normal equation은 learning rate값이 필요없으며
반복도 필요없는 장점이 있지만
계산비용이 커서 n(특성 개수)이 커지면 매우 느려진다.
Coursera강의에서는 n이 10000정도쯤 되면 Gradient Descent를 하는 것이 낫다고 한다.
'Machine Learning > coursera' 카테고리의 다른 글
| Classification (0) | 2016.02.29 |
|---|---|
| Vectorization (0) | 2016.02.22 |
| Cost Function - Intuition (2) | 2016.02.08 |
| Linear Regression with one variable - Cost Function (0) | 2016.01.25 |
| Unsupervised Learning (0) | 2016.01.25 |























