원문 : http://www.songho.ca/opengl/gl_projectionmatrix.html
Overview
컴퓨터 모니터는 평면이다. OpenGL에서 렌더링된 3d장면은 2d이미지로 컴퓨터 스크린에 투영되야 한다. GL_PROJECTION 행렬은 이 투영변환에 사용된다. (OpenGL 2.0부터 쉐이더를 사용하므로 투영행렬로 생각하자.) 처음에 투영행렬은 모든 vertex data를 카메라 좌표로부터 clip좌표로 변환시킨다. 그리고 이 clip좌표는 또한 w요소로 나누는 것에 의해 normalized device coordinates (NDC, 정규좌표)로 변환된다.
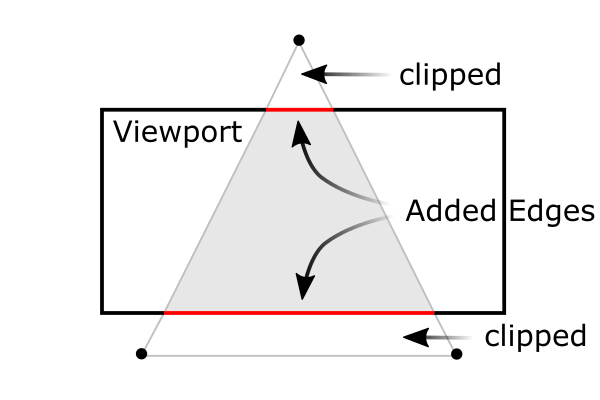 A triangle clipped by frustum
A triangle clipped by frustum따라서 우리는 NDC 변환과 clipping(절두체 자르기?)가 투영행렬로 통합되는 것을 기억해야한다. 앞으로의 섹션들은 left, right, bottom, top, near, far 이 6개의 파라미터들로 부터 어떻게 투영행렬을 얻는지 설명한다.
clipping은 wc로 나누기 전에 clip좌표에서 수행된다는 것을 기억해라. clip좌표 xc, ycand zc 는 wc와 비교함으로 테스트된다. 어떤 클립좌표가 -wc보다 작거나 wc보다 크면 그 vertex는 폐기될 것이다.
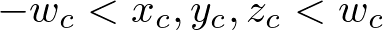
그러면 OpenGL은 클리핑이 발생하는 다면체의 면을 재구성할 것이다.
Perspective Projection
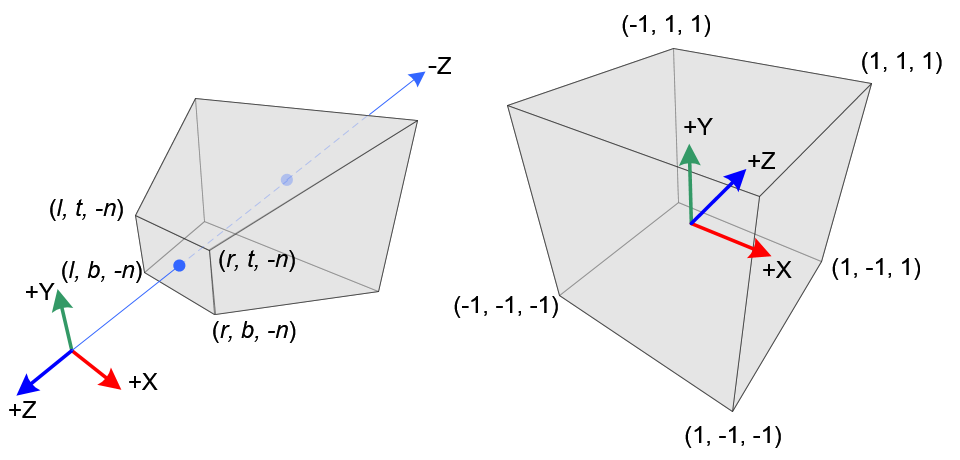 Perspective Frustum and Normalized Device Coordinates (NDC)
Perspective Frustum and Normalized Device Coordinates (NDC)원근 투영에서 끝이 잘린 피라미드내 한 3차원 점은 큐브(NDC)로 매핑된다. x축 좌표계의 범위는 [l, r] 에서 [-1, 1]로 y는 [b, t]에서 [-1, 1]로 그리고 z는 [n, f]에서 [-1, 1]로 (왼쪽 그림과 같이)
카메라 좌표계는 오른손 좌표계에서 정의되지만(opengl이라서) NDC는 왼손 좌표계를 사용한다. 이것은 원래 카메라는 -Z축을 바라보지만 NDC에서는 +Z축을 바라보는것을 의미한다. glFrustum()는 near, far 거리값을 양수만 취하기 때문에 투영행렬을 유도하는 동안 부호를 바꿀 필요가 있다.
OpenGL에서 카메라공간상의 한 점은 near평면으로 투영된다. 아래 그림은 어떻게 카메라공간상에서 점(xe, ye, ze)가 near평면 위 (xp, yp, zp)로 투영되는지 보여준다.
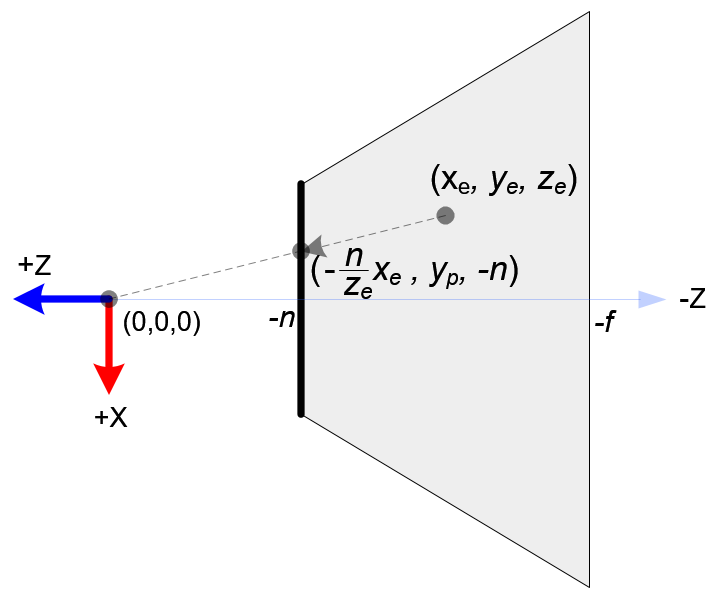 Top View of Frustum
Top View of Frustum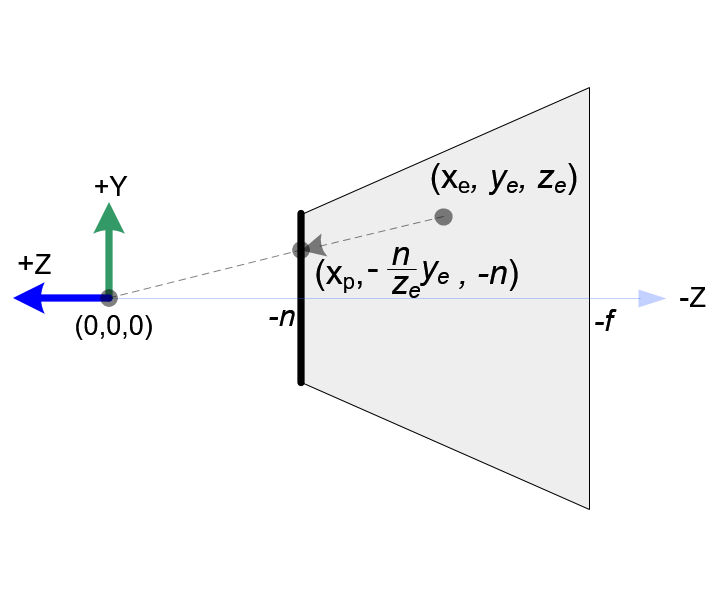 Side View of Frustum
Side View of Frustum절두체를 위에서 볼때 xe는 삼각형의 닮음비에 의해 계산된 xp로 매핑된다.
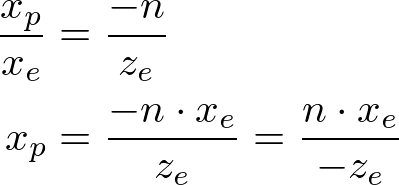
옆에서 볼때 yp 또한 같은 방식으로 계산한다.
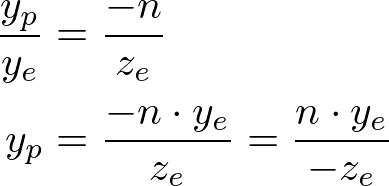
xp와 yp는 ze에 의존한다. 역으로 둘다 -ze에 비례한다. 즉 둘다 -ze로 나눠진다. 이는 투영행렬을 유도하는데 중요한 첫 단서이다. 카메라 좌표가 투영행렬을 곱함으로 변환된 이후에 클립 좌표는 여전히 동종의 좌표이다. 클립 좌표의 w요소로 나누는것으로 정규좌표(NDC)가 된다. (See more details on OpenGL Transformation.)
 ,
, 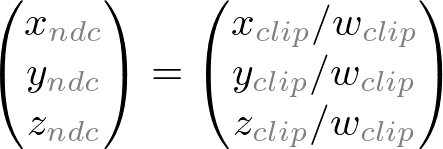
그러므로 우리는 클립 좌표의 w요소를 -ze으로 설정할 수 있다. 그러면 투영행렬의 4번째 행은 (0, 0, -1, 0)이 된다. ([-1, 1]로 매핑되기 때문이며 이 값으로 나누어 NDC로 변환된다.)
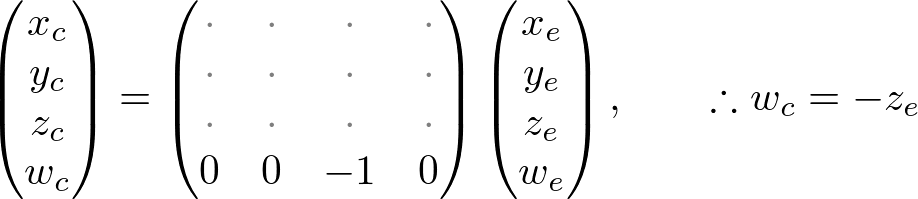
그 다음에 xp와 yp를 NDC의 xn와 yn으로 선형관계에서 매핑한다. [l, r] ⇒ [-1, 1] and [b, t] ⇒ [-1, 1].
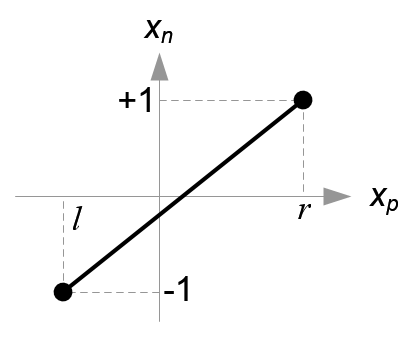 Mapping from xp to xn
Mapping from xp to xn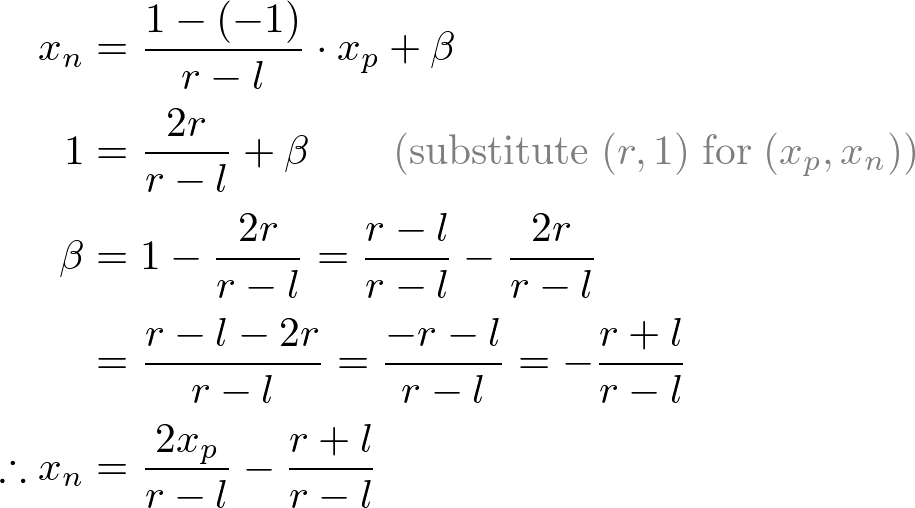
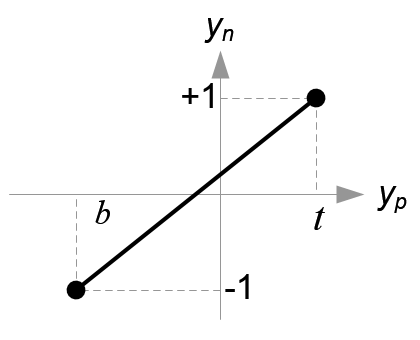 Mapping from yp to yn
Mapping from yp to yn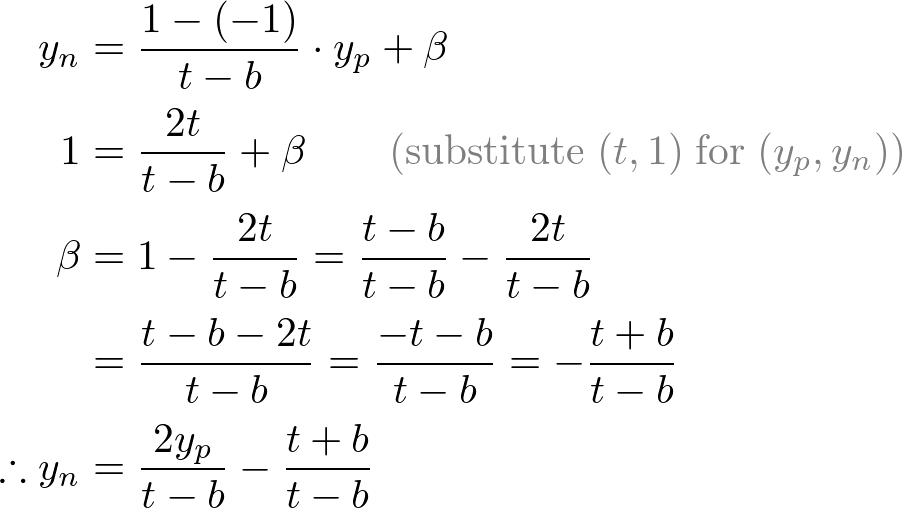
xp와 yp를 위 방정식으로 교체한다.
원근 분할(xc/wc, yc/wc)에 대해 -ze로 나누어지는 두 방정식을 얻었다. 그리고 wc를 미리 -ze로 설정했다. 위 방정식의 괄호 안 부분들이 클립 좌표의 xc, yc가 된다.
이것으로부터 우리는 투영행렬의 첫번째행과 두번째행을 구할 수 있다.
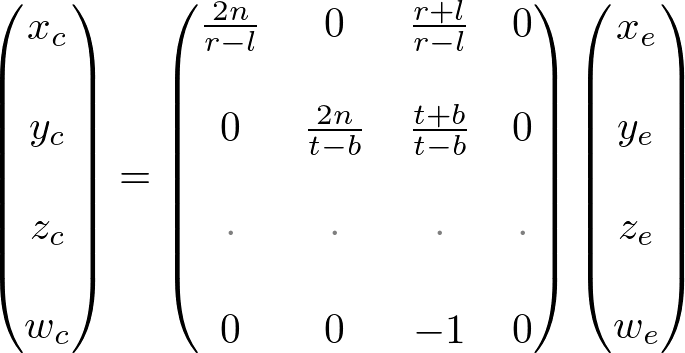
이제 투영행렬의 세번째행만 남았다. zn를 구하는 것은 조금 다르다. 왜냐하면 카메라 좌표상의 ze는 항상 near평면의 -n으로 투영되기 때문이다. 하지만 우리는 클리핑과 깊이 테스트를 위한 특별한 z값이 필요하다. 또 unproject(역변환. 투영행렬의 역행렬을 취하여 투영되기 전의 점을 구하는 듯)을 할 수 있어야 한다. z가 x나 y값에 의존하지 않는 것을 알기 때문에 zn와 ze사이 관계를 알기 위해 w요소를 차용한다. 그러면 이런식으로 투영행렬의 세번째 행을 명시할 수 있다.
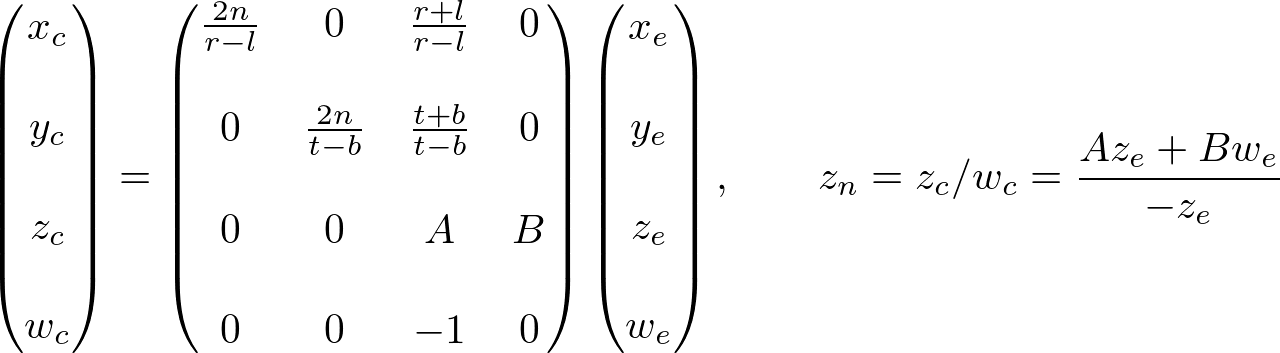
카메라 공간에서 we는 1이므로 방정식은 이렇게 된다.
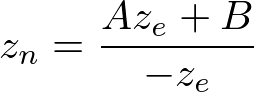
계수 A, B를 구하기 위해 (ze, zn)의 관계 (-n, -1)와 (-f, 1)를 이용한다. 그리고 위 방정식에 넣어서 연립장정식을 풀 수 있다.
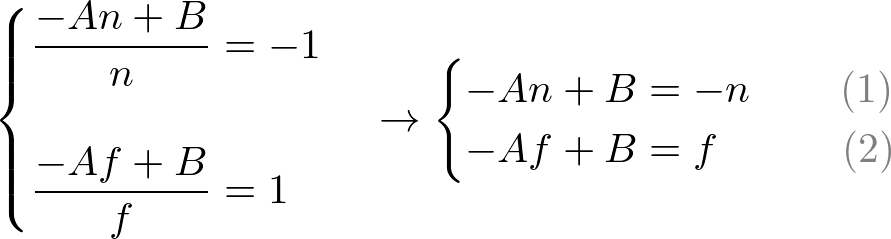
A와 B에 대해 방정식을 풀기 위해 (1)식을 B에 대하여 다시 쓰면
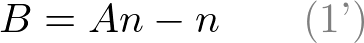
식(1')을 식(2)의 B로 교체하여 A에 대하여 풀면
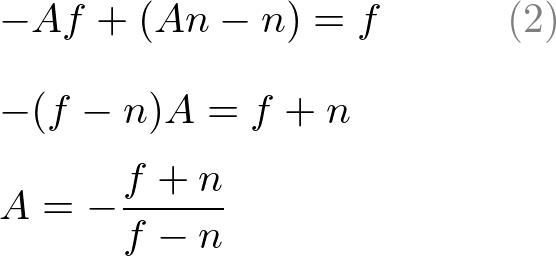
구한 A를 식(1)에 넣어서 B를 구한다.
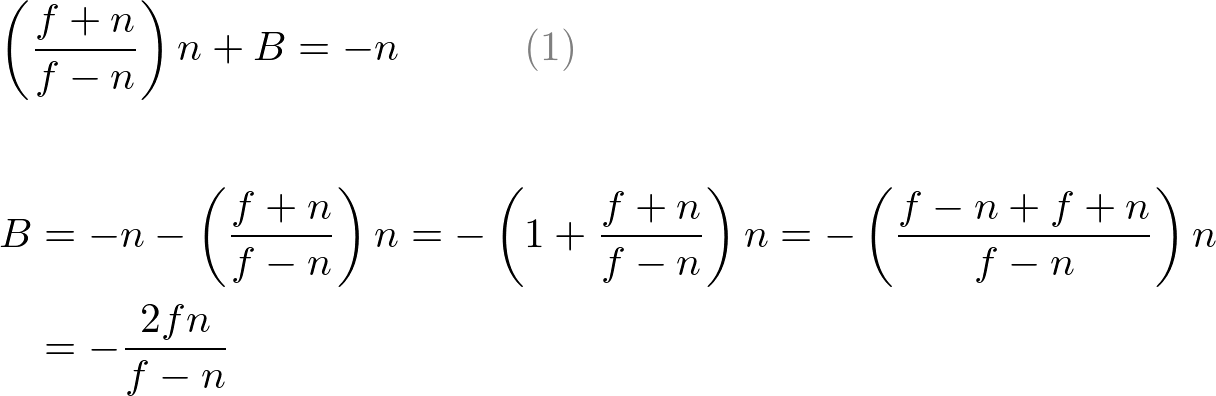
A와 B를 구했으므로 ze, zn사이 관계는 이렇게 된다.
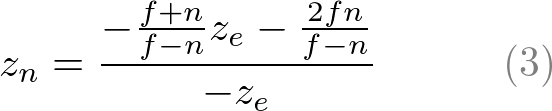
마침내 투영행렬 전체를 구하였다. 완성된 행렬의 모습이다.
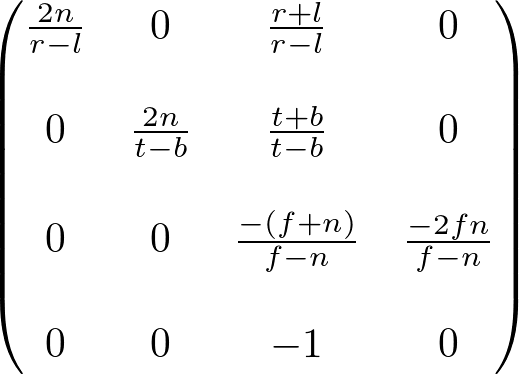
OpenGL Perspective Projection Matrix
이 투영 행렬은 일반적인 절두체에 대해서이다. 만약 viewing 공간이 좌우 대칭 즉, 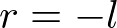 and
and 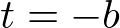 이면 이렇게 간략하게 표현할 수 있다.
이면 이렇게 간략하게 표현할 수 있다.
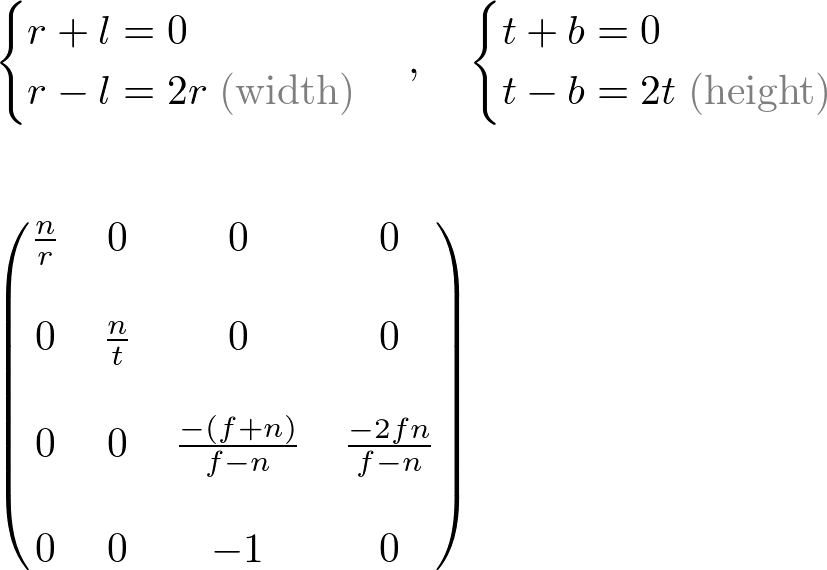
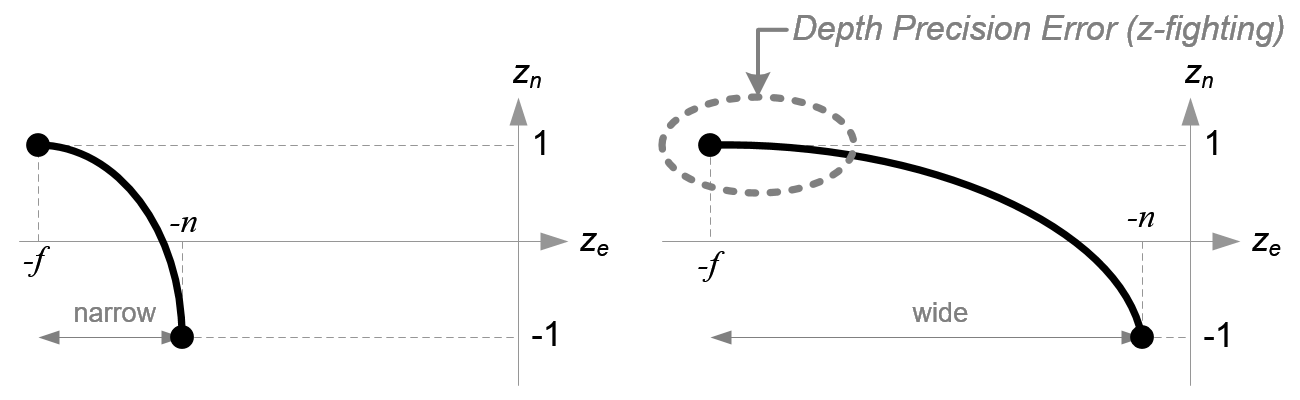
마치기 전에 식(3)의 ze, zn관계를 다시 한 번 보기 바란다. 관계가 비선형관계이며 유리함수라는 것을 알 수 있다. 이것은 near평면에서 매우 정확하지만 far평면에서는 매우 부정확하다는 것을 의미한다. 만약 [-n, -f]범위가 매우 크다면 깊이 정확도 문제(z-fighting)를 초래할 수 있다. far평면 근처에서 ze의 작은 변화는 zn값에 영향을 미치지 않는 문제이다. z-fighting을 최소화하기 위해 가능한한 near와 far사이 거리는 작아야 한다.
Comparison of Depth Buffer Precisions
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
국어도 못하는데 외국어를 번역하려하니 어려운 것 같다.


















![[-\infty,+\infty]](https://upload.wikimedia.org/math/9/3/6/936cbe1fb6394ff85b26a5e76e81fcd5.png)


 이다.
이다.




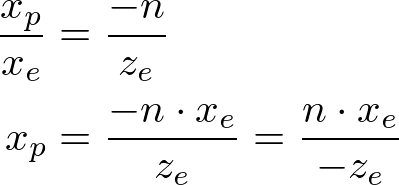
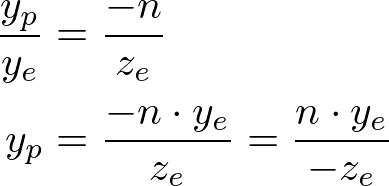
 ,
, 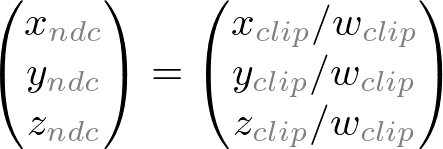
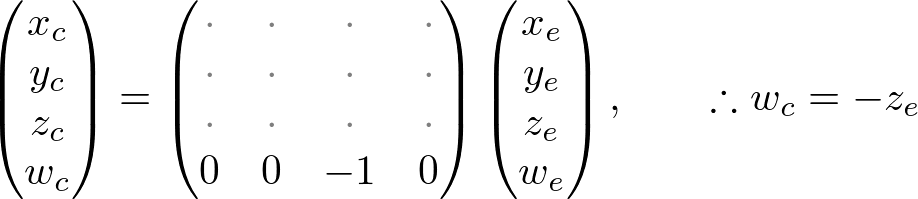

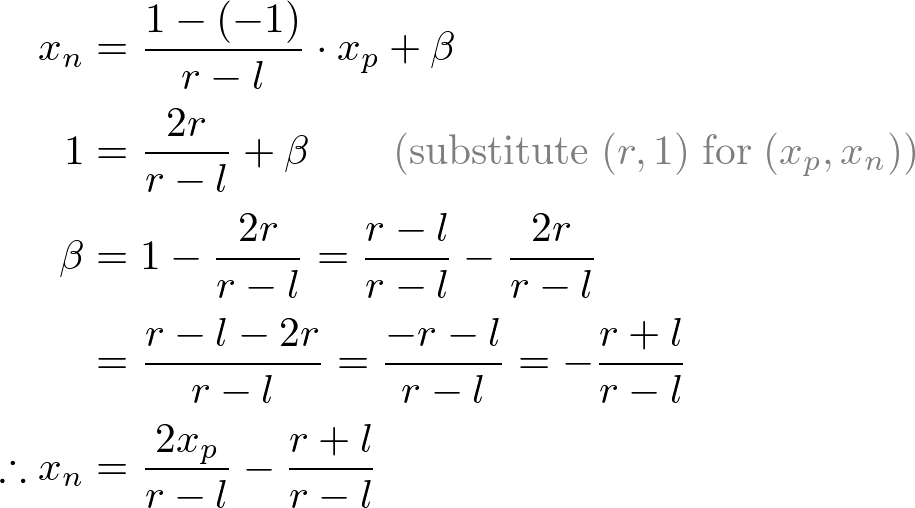

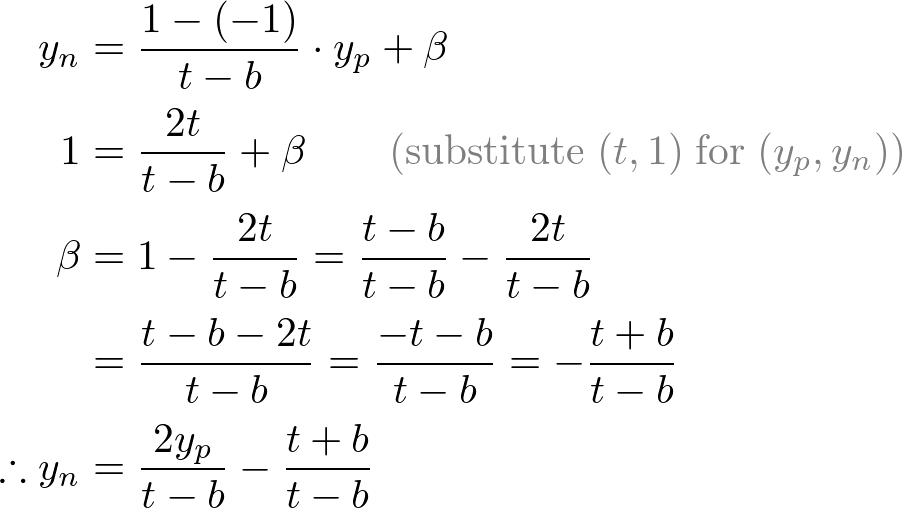
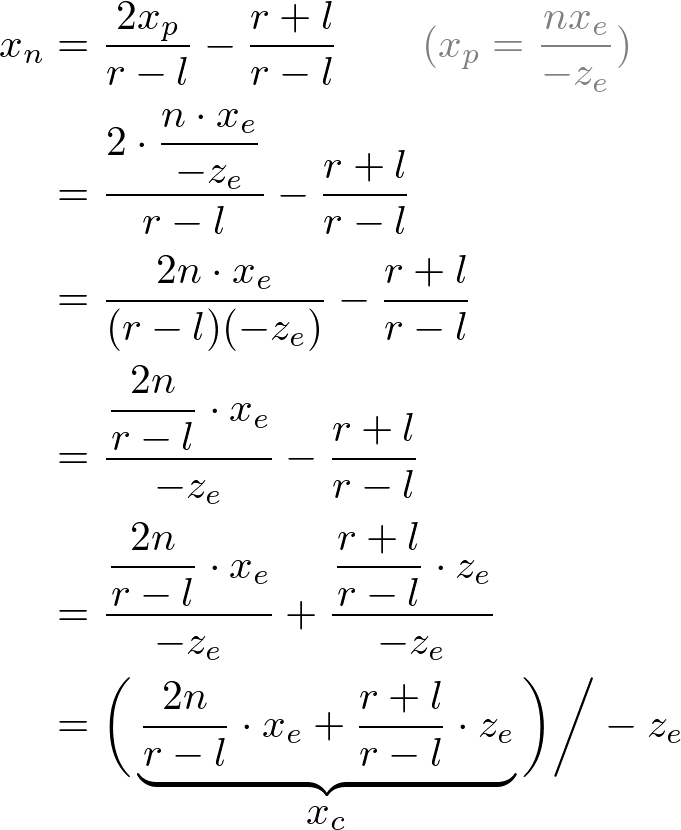
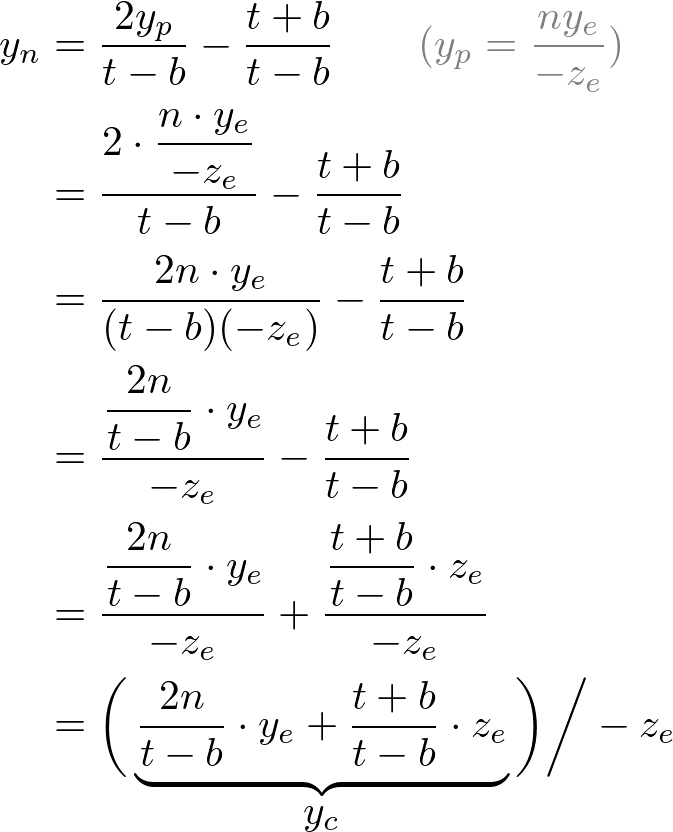
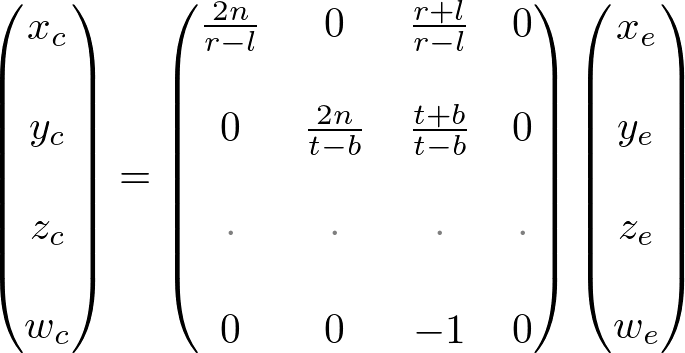
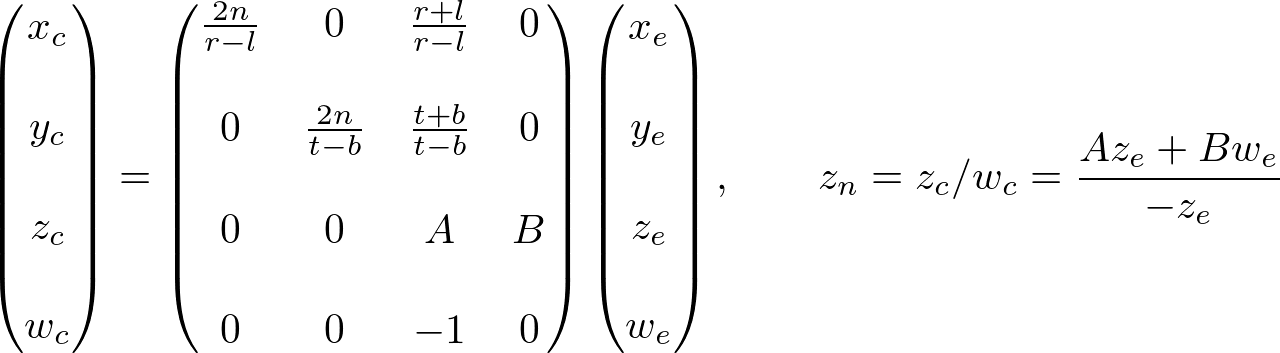
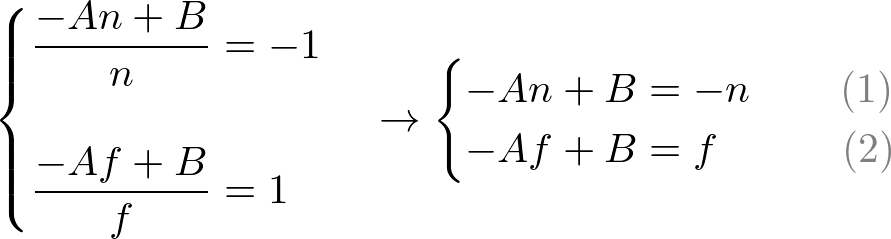
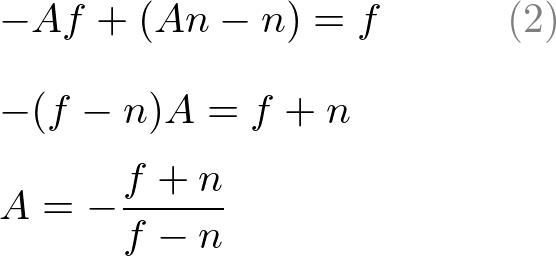
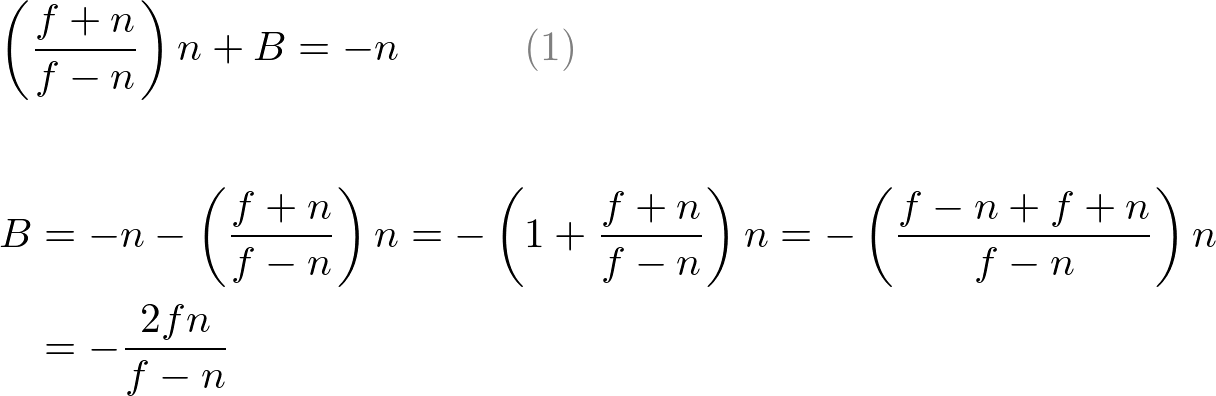
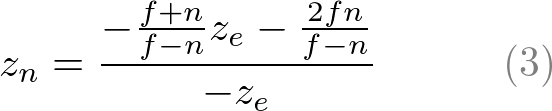
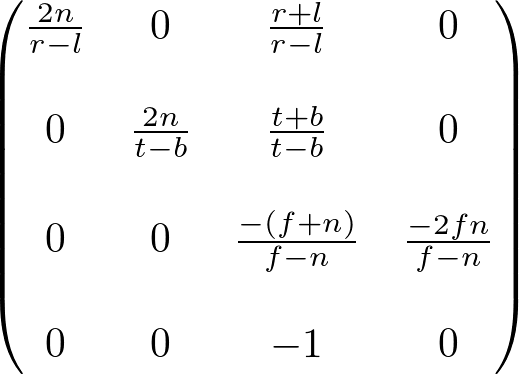
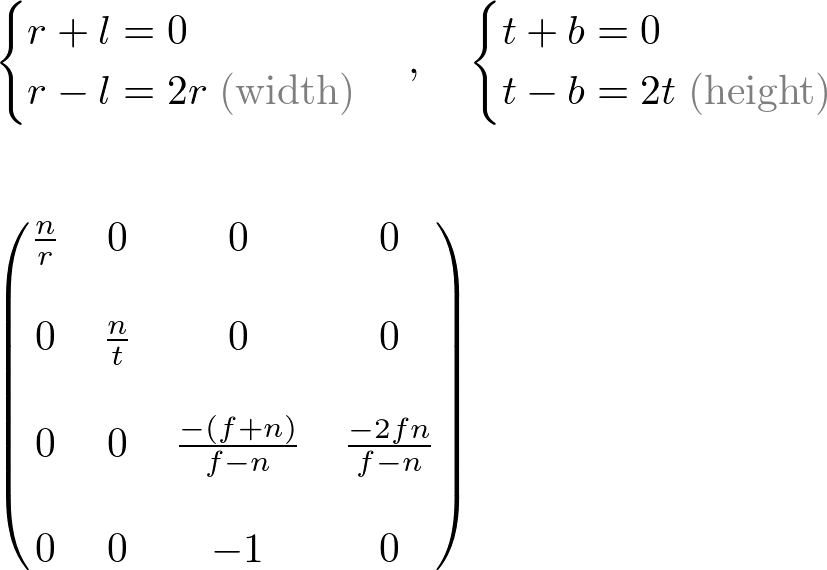
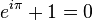

 와
와  의 벡터곱은
의 벡터곱은  라 쓰고, 다음과 같이 정의된다. (위키백과)
라 쓰고, 다음과 같이 정의된다. (위키백과)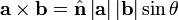

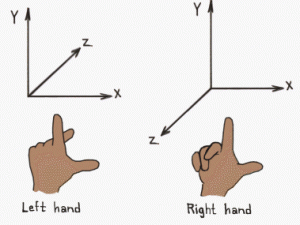
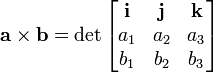
![\mathbf a \times \mathbf b = [a_2 b_3 - a_3 b_2, a_3 b_1 - a_1 b_3, a_1 b_2 - a_2 b_1]](https://upload.wikimedia.org/math/8/3/a/83ae8e654ce1d91560874d536ef95d15.png) 이 된다.
이 된다.


