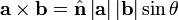벡터의 외적과 삼중곱

2015. 6. 26. 12:13

벡터곱

두 벡터 $\mathbf{a}$ 와 $\mathbf{b}$ 의 벡터곱은 $\mathbf{a} \times \mathbf{b}$ 라 쓰고, 다음과 같이 정의된다. (위키백과)

\mathbf{a} \times \mathbf{b} = \hat{\mathbf n} \left| \mathbf{a} \right| \left| \mathbf{b} \right| \sin \theta

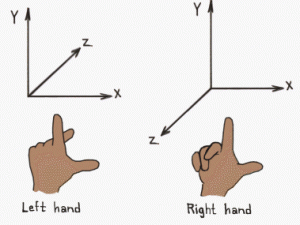
단위벡터 n은 벡터a와 벡터b에 공통수직으로 아래 그림과 같이 두개가 나온다.

해서 좌표계에 따라 정한다. (위 그림은 오른손 좌표계. 나사 돌리듯 벡터a에서 벡터b로 회전한다고 생각하면 된다.)

Left-handed and right-handed coordinate systems. Source: http://viz.aset.psu.edu/gho/sem_notes/3d_fundamentals/html/3d_coordinates.html

opengl(오른손좌표계), directx(왼손좌표계)

벡터a와 벡터b사이의 각을 계산할 필요없이 행렬식을 이용하여

아래 행렬의 1행에 대한 "여인수(cofactor)"를 전개하면 벡터의 좌표를 구할 수 있다.

(i x j = k, j x k = i, k x i = j 인 단위벡터)

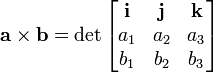
$\mathbf{a}\times\mathbf{b}=\det \begin{bmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ \end{bmatrix}$

곧

$\mathbf a \times \mathbf b = [a_2 b_3 - a_3 b_2, a_3 b_1 - a_1 b_3, a_1 b_2 - a_2 b_1]$ 이 된다.

#############################################################################################

외적의 크기

#############################################################################################

벡터 삼중곱

{\mathbf {a}}\times ({\mathbf {b}}\times {\mathbf {c}})={\mathbf {b}}({\mathbf {a}}\cdot {\mathbf {c}})-{\mathbf {c}}({\mathbf {a}}\cdot {\mathbf {b}})

({\mathbf {a}}\times {\mathbf {b}})\times {\mathbf {c}}=-{\mathbf {c}}\times ({\mathbf {a}}\times {\mathbf {b}})=-{\mathbf {a}}({\mathbf {b}}\cdot {\mathbf {c}})+{\mathbf {b}}({\mathbf {a}}\cdot {\mathbf {c}}).

(라그랑주 공식)

증명:

--------------------------------------------------------------------------------------------------

임의의 축 회전 (Axis Angle Rotation) (0)	2016.09.30
선형 보간(lerp)과 구면 선형 보간(slerp) (0)	2016.06.11
로지스틱 함수 (0)	2016.03.17
Perspective Projection Matrix(원근 투영 행렬)의 유도 (0)	2016.01.31
오일러 공식(Euler fomula) (0)	2016.01.05

고귀양이의 노트.