로지스틱 함수

로지스틱 함수

독립 변수(hypothesis에서 x, 즉 feature)가 [-∞,∞]의 어느 숫자이든 상관 없이 종속 변수(y) 또는 결과 값이 항상 범위 [0,1] 사이에 있도록 한다. 이는 오즈비(odds ratio)를 로짓(logit) 변환을 수행함으로써 얻어진다.

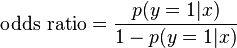
성공확률이 실패할 확률보다 얼마나 높은가에대한 비율이다.

odds ratio에 로그를 취한 형태의 함수로 입력값이  일 때 출력 값의 범위를 [0,1]로 조정한다.

logit 변환의 그래프

로지스틱 함수는 선형 회귀(linear regression)에서 비롯되었다.

그래서 로지스틱 회귀에서 로짓 변환의 결과와 선형 예측 함수(coursera에서 hypothesis)의 결과값이 같다.

그러므로  으로 표현할 수 있다.

따라서 구하고자 하는 특정 독립 변수 x가 주어졌을 때 종속 변수가 1인 카데고리에 속할 확률은

 이다.

logistic 함수

--------------------------------------------------------------------------------------------------------------------

위키백과