728x90
아래와 같은 모양의 오일러 공식은 1748년 오일러가 무한급수의 좌우 극한값이
같음을 증면하면서 발표되었다. (위키백과)
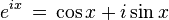
(여기서, e는 자연로그의 밑인 상수이고, i는 제곱하여 -1이 되는 허수단위이다.)
위 식의 x 에 파이를 넣으면
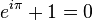 라는
라는
"오일러 등식"을 얻을 수 있다.
또한
오일러 공식에서 x 에 a+b를 넣으면
이 된다.
위 식은 이렇게도 표현 할 수 있다.
식을 정리하면
이 되므로
으로 삼각함수의 덧셈정리를 증명할 수 있다.
728x90
'수학' 카테고리의 다른 글
| 임의의 축 회전 (Axis Angle Rotation) (0) | 2016.09.30 |
|---|---|
| 선형 보간(lerp)과 구면 선형 보간(slerp) (0) | 2016.06.11 |
| 로지스틱 함수 (0) | 2016.03.17 |
| Perspective Projection Matrix(원근 투영 행렬)의 유도 (0) | 2016.01.31 |
| 벡터의 외적과 삼중곱 (0) | 2015.06.26 |
