ball tree도 kd tree와 마찬가지로 knn(k-nearest neighbor) search에 많이 쓰이는 트리이다.
kd tree보다는 초기 트리 구성에 비용이 크지만, kd tree의 경우 차수가 아주 크면
query했을때 검색이 매우 느려지는데, ball tree는 kd tree보다 훨씬 빠르게 결과를 도출한다.
a(1,1550), b(900,440), c(2500,330), d(4000,2), e(5000,1)
위와 같은 데이터가 주어졌을때의 트리의 구성은 그림과 같다.
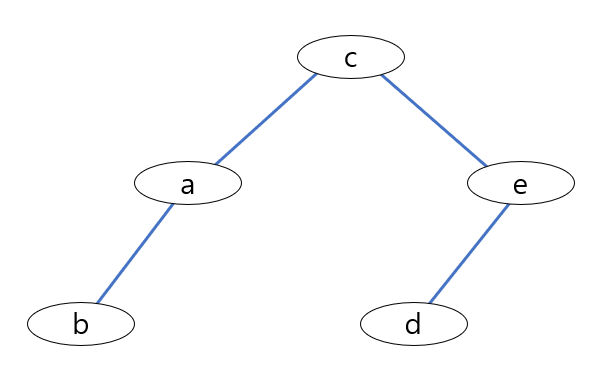
먼저 가장 범위가 큰 차수로 정렬을 시키고 (위 데이터에서는 1번째 차원의 범위가 1~5000이므로 가장 크다)
중간값을 취하고 왼쪽, 오른쪽으로 나눈 뒤 다시 재귀적으로 트리를 구성하도록 한다.
검색에 활용하도록 반지름 값도 구하는데 자식 노드중 가장 멀리 떨어진 노드와의 거리가 반지름이 된다.
이때, leaf size가 1보다 큰 경우 중간값을 size만큼의 개수를 취한다.
(leaf size는 검색 결과에 영향은 없지만 검색 속도에 영향이 있을 수 있다.)
예시 데이터를 기반으로 'ball'을 그려보면 다음과 같을 것이다.
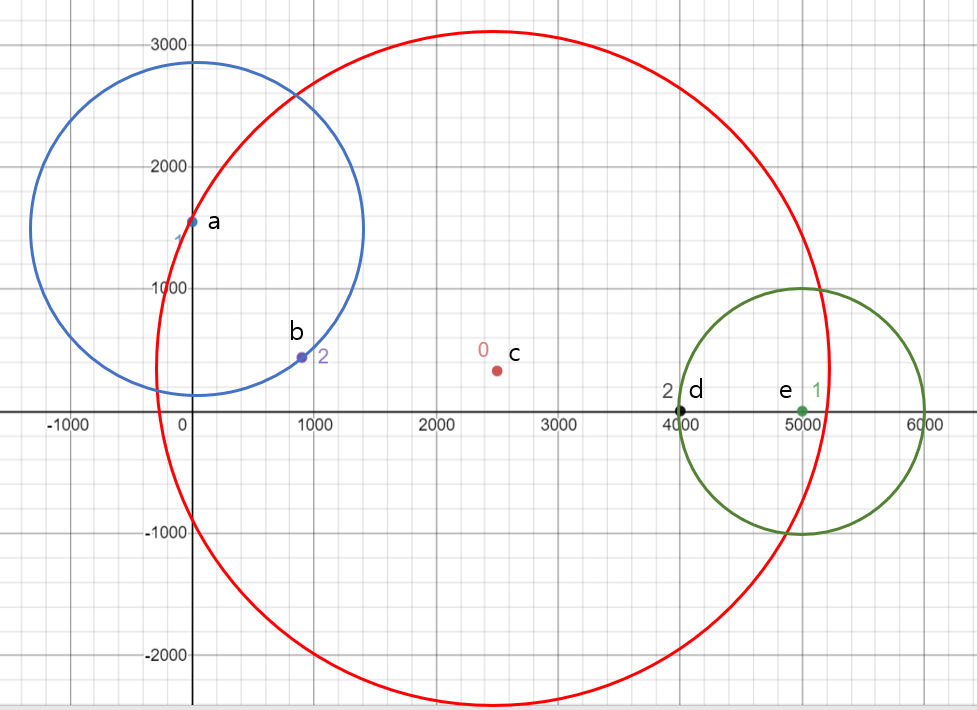
알고리즘 설명및 코드의 한글 자료는 거의 전무하여 (내 검색 능력이 모자른 것일 수도)
위키백과와 사이트의 내용을 참고하였다.
import numpy as np
class Node:
def __init__(self, data, radius, depth, left_child=None, right_child=None):
self.left_child = left_child
self.right_child = right_child
self.data = data
self.radius = radius
self.depth = depth
def printALL(self):
print(self.radius, self.data, self.depth)
if self.left_child != None:
self.left_child.printALL()
if self.right_child != None:
self.right_child.printALL()
def balltree(ndata, depth):
if ndata.shape[0] < 1:
return None
# element가 한 개일 경우
if ndata.shape[0] == 1:
return Node(
data=np.max(ndata, 0).tolist(),
radius=0,
depth=depth,
left_child=None,
right_child=None
)
else:
# 범위가 가장 큰 dimension에 따라 정렬
largest_dim = np.argmax(ndata.max(0) - ndata.min(0))
i_sort = np.argsort(ndata[:, largest_dim])
ndata[:] = ndata[i_sort, :]
nHalf = int(ndata.shape[0] / 2)
loc = ndata[nHalf, :]
data = loc.tolist()
# 중간 값(data)에서 가장 멀리 떨어진 값 까지의 거리
radius = np.sqrt(np.max(np.sum((ndata - loc) ** 2, 1)))
return Node(
data=data,
radius=radius,
depth=depth,
left_child=balltree(ndata[:nHalf], depth+1),
right_child=balltree(ndata[nHalf+1:], depth+1)
)
if __name__ == '__main__':
X = [[1,1550], [900,440], [2500,330], [4000,2], [5000,1]]
X = np.asarray(X)
tree = balltree(X, 0)
tree.printALL()역시 파이썬 패키지중 sklearn에서 balltree의 생성 및 검색을 간편하게 할 수 있다.
결과로 가장 유사한 데이터의 인덱스 번호와 거리를 반환한다.
import numpy as np
from sklearn.neighbors import BallTree
X = [[1,1550], [900,440], [2500,330], [4000,2], [5000,1]]
X = np.asarray(X)
# 트리 생성
tree = BallTree(X)
# 테스트 데이터 쿼리
dist, ind = tree.query([[1, 1551]], 1)
print(dist, ind)
-----------------------------------------------------------------------------------------------------------------------------------
참고
https://en.wikipedia.org/wiki/Ball_tree
Ball tree - Wikipedia
This article is about the binary tree variant. For a metric-tree involving multi-way splits, see M-tree. In computer science, a ball tree, balltree[1] or metric tree, is a space partitioning data structure for organizing points in a multi-dimensional space
en.wikipedia.org
https://www.astroml.org/book_figures/chapter2/fig_balltree_example.html
Ball Tree Example — astroML 0.4 documentation
Ball Tree Example Figure 2.5. This example creates a simple Ball tree partition of a two-dimensional parameter space, and plots a visualization of the result. # Author: Jake VanderPlas # License: BSD # The figure produced by this code is published in the t
www.astroml.org
'프로그래밍 > Python' 카테고리의 다른 글
| flask-admin 에서 pk, fk 등이 보이지 않고, 수정, 추가 안될때 해결 방법 (0) | 2023.05.01 |
|---|---|
| lof (0) | 2019.08.26 |
| kd tree (1) | 2019.07.04 |
| keras를 활용한 다중선형회귀분석 (2) | 2019.05.30 |
| [python] 디렉토리내 파일 이름 변경 (1) | 2015.09.07 |