DFS는 그래프나 트리에서 탐색하는 대표적인 두가지 방법(DFS, BFS)중 하나로, 하위 혹은 연결된 노드 중 하나를
우선적으로 방문하는 형태이다. 여기에서는 무방향 그래프를 사용하여 알아 보도록 한다.
인접 행렬, 인접 리스트
먼저 그래프의 구현에 앞서 인접 행렬과 인접 리스트가 있다.
인접 행렬의 경우 NxN의 행렬로(N은 노드 개수)로 표시하는 것으로, 다음과 같이 표시한다.
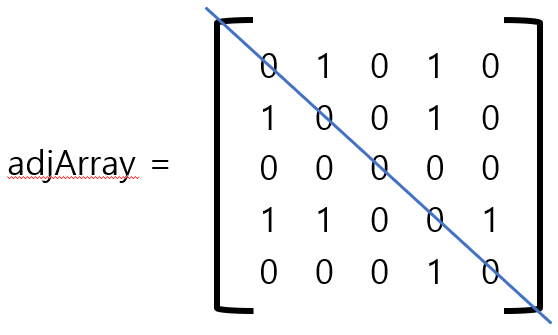
0, 1의 노드가 연결되어 있는 경우, adjArray[0][1] = 1로 표시한다.
무방향 그래프의 경우 인접 행렬의 대각선(푸른선)을 기준으로 뒤집어진 대칭을 이루고 있다.
현재 행렬값이 모두 1로 되어 있지만 가중치 그래프의 경우 행렬의 숫자를 바꾸면 된다.
장점 :
구현이 비교적 간단하다.
i, j노드의 연결을 확인할 경우 adjArray[i][j]로 바로 확인할 수 있어, O(1)의 시간복잡도를 가진다.
단점 :
i 노드에 연결된 모든 노드를 확인하고자 할때 adjArray[i][0] ~ adjArray[i][N-1] 모두 확인해야해서
O(N)의 시간복잡도를 가진다. 노드가 많고 간선(연결)이 적을때 비효율이다.
공간복잡도도 O(N^2)로 메모리를 많이 차지한다.
인접 리스트의 경우 연결된 노드들의 리스트로 다음과 같이 표현한다.

0, 1의 연결을 확인하고 싶은 경우 adjList[0] 리스트를 순회하여 1번이 있는 지 확인하면 된다.
무방향의 경우 인접 행렬과 동일하게 0, 1이 연결된다면 1, 0의 연결도 추가하여야 한다.
장점 :
i와 연결된 모든 노드를 확인하고자 할때 최악의 경우(i가 모든 노드와 연결된 경우) O(N)이지만,
대부분의 경우 항상 O(N)인 인접행렬보다 빠르다.
공간복잡도도 간선의 개수를 E라 할때 최악의 경우를 제외하고 O(E) < O(N^2)이므로 낭비가 적다.
단점 :
i, j의 연결을 확인하고 싶을때 adjList[i]를 순회하며 j가 있는지 봐야 하므로 O(N)으로 인접행렬보다 느리다.
DFS
dfs의 동작을 간단하게 보면 다음과 같다.


2번 노드 부터 시작하면 먼저 스택에 2를 푸쉬해 둔다.
1. pop하여 스택 최상단 노드를 꺼내어 방문 표시를 하고 출력한다.
2. 해당 노드의 인접 노드중 미방문 노드를 전부 push한다. 이때 스택에 중복 push는 없게 한다.
2. 스택이 빌때까지 1, 2번을 계속한다.
예시 그래프의 노드를 위 순서대로 진행하면 2 1 0 3 4가 된다.
코드
함수 호출이 스택메모리를 사용하므로 재귀호출로도 구현할 수 있다.
이번 코드에서는 JAVA에서 지원하는 stack 컨테이너로 구현하였다.
스택에 중복 데이터에 대한 예외처리를 하지 않았기 때문에 탐색 순서가 다르게 나올 수 있다.
(스택에 들어있는지 확인하는 행렬 같은 거를 추가하면 쉽게 구현할 수 있다.)
import java.util.*;
public class graph {
private int szVertex;
private ArrayList<Integer> adjList[];
private boolean visited[];
private Stack<Integer> stack; // for DFS
public graph(int v) {
szVertex = v;
visited = new boolean[szVertex]; // default false
adjList = new ArrayList[szVertex];
for (int i = 0; i < szVertex; i++) {
adjList[i] = new ArrayList();
}
stack = new Stack();
}
public void addEdge(int from, int to) {
// 무방향 그래프이므로 반대의 경우도 추가
adjList[from].add(to);
adjList[to].add(from);
}
// 재귀 호출로 구현할 수 있지만 stack을 이용하여 구현하였다
public void DFS(int start) {
stack.push(start);
// stack이 비어질때까지 게속
while (!stack.isEmpty()) {
// stack 최상단을 꺼내어 방문 행렬에 표시하고 출력
int current = stack.pop();
// 미방문 정점의 경우
if (!visited[current]) {
visited[current] = true;
System.out.print(current + " ");
// 인접 리스트에서 미방문 정점의 경우 스택에 추가
for (int i : adjList[current])
if (!visited[i])
stack.push(i);
}
}
System.out.println();
}
// 첫노드가 주어지지 않을 경우 0번 부터
public void DFS() {
DFS(0);
}
}public class dfs {
public static void main(String[] args) {
graph g = new graph(5);
g.addEdge(0, 4);
g.addEdge(1, 3);
g.addEdge(2, 4);
g.addEdge(2, 3);
g.addEdge(1, 2);
g.addEdge(1, 0);
g.DFS(2);
}
}'프로그래밍 > Java' 카테고리의 다른 글
| 다익스트라(Dijkstra) 알고리즘 (0) | 2019.10.26 |
|---|---|
| 너비 우선 탐색(BFS) (0) | 2019.10.21 |
| [Android] 사설 SSL 인증서를 이용한 https 통신 (4) | 2018.05.30 |
| [JAVA] NFC 제어 (2) | 2017.10.15 |
| [Android] HCE를 이용한 NFC 통신 (8) | 2017.10.15 |