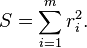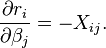고귀양이의 노트.

Representation

뉴럴 네트워크는 딥러닝의 토대가 되는 기술로 동물의 뇌의 뉴런의 행위를 모방한 알고리즘이다.

위 사진은 뉴런을 도식화 한 것인데 Dendrite는 외부로부터의 전기신호를 받는 "input wires"이고

Axon은 Nuclues에서 가공이 된 신호를 외부로 보내는 "output wire"가 된다. 이는 매우 함수의 형태와 비슷한데

기존의 2진 로지스틱에 빗대어 보면 왼쪽 그림처럼 표현할 수 있겠다.

(타 강의나 프레임워크에서의 표현과 달리 앤드류응교수님의 강의는

'x0 = 1'인 열을 추가해서 'X*∂+b'가 아니라 'X*∂'인 것이

가끔 헷갈리네요 ㅠㅠ 멍청한가 봅니다.)

단일 뉴런의 형태를 위와 같이 표현하면 뉴럴 네트워크란 여러 뉴런이 연결되어있는 것처럼

위의 형태를 다수 연결하여 그룹이 된 것이다.

왼쪽 그림처럼 input으로 x1, x2, x3이 있고 각 뉴런 a1, a2, a3에 넣어주고 있다.

그리고 그 결과를 다시 마지막 뉴런에 보낸다.

이것이 뉴럴 네트워크인 것인다.

(뉴럴 네트워크에서 Layer1은 input layer,

마지막 Layer3은 output layer라 부르며

그 사이의 모든 layer는 hidden layer라고 부른다. 단일 뉴런(로지스틱)에서 처럼

학습셋업시 input의 X벡터와 output의 h(x)의 결과와 y값과의 차이 외에는

보지 않기 때문이다.)

위 뉴럴 네트워크의 hypothesis를 표현하면 이렇게 된다.

여기서 g는 로지스틱 함수이며 bias값을 위한 x0를 포함한 X벡터가 각 Layer2의 뉴런들에 들어가서 그 결과인

a1, a2, a3가 다시 최종 레이어의 input으로 들어가는 형태이다. (물론 bias를 위해 a0가 추가된다.)

이걸 벡터화 해서 표현하면

이렇게 될 것이다.

더 간단히 수식으로 표현하면:

z(j+1)=Θ(j)a(j)

hΘ​(x)=a(j+1)=g(z(j+1))

이 된다.

XOR 문제

xor 문제(혹은 xnor)문제는 선형적으로는 풀 수 없다.

xor를 뉴럴네트워크(이하 NN)가 해결할 수 있으면

오른쪽 그래프와 같은 복잡한 문제도 해결 할 수 있을 것이다.

다른 논리 연산들은 대부분 선형적으로(단일 뉴런) 풀 수 있다.

대표적으로 AND를 예로 들면

∂0 = -20, ∂1 = +20, ∂0 = +20이라 가정할때 오른쪽 표와 같은 결과를

얻을 수 있을 것이다. 

OR나 NOT등의 논리 연산 또한 선형적으로 구할 수 있으며

결록적으로 XNOR은 이러한 논리연산들을 연결하여 구할 수 있다.

진리표로 예를 들자면

(편의상 c언어의 비트연산자로 표현)

쉽게 알 수 있다. 이처럼 각 논리연산을 하는 뉴런을 연결하면 아래와 같이 될 것이다.

이로 인해 XNOR문제는 NN을 이용해 풀 수 있는 것을 보았다.

마찬가지로 XOR 또한 NOT레이어를 더 추가하든, 최종 결과값을 뒤집든 해서 동일하게 구할 수 있음을 알 수 있다.

학습된 데이터를 기반으로 위와 같이 데이터의 그룹을 분류하는 것이 목적이다.

'선형회귀' 방식으로 가정식을 세우고 직선을 구하면 위와 같을 것이다.

여기서 0.5를 한계점으로 두고 가정식이 0.5보다 크거나 같으면 악성

0.5보다 작으면 양성이라고 판달할때 현재는 0.5를 기준으로 잘 나뉘어 진 것 같다.

여기서 데이터를 추가하면

새로운 데이터(파란색 X) 가 들어올 경우 가정식은 위와 같이 바뀔 것이다.

그리고 우리의 한계점이 이동하게 되어 직감적으로 별초 좋치 못 해 보인다.

이전 분홍색 가정식에 비해 경계선도 깔끔하지 않은 것 같다. 이러한 이유로

Classification에서는 선형회귀를 사용할 수 없다.

대신에 Logistic regression (로지스틱 회귀분석)을 일반적으로 사용한다.

로지스틱 함수란?

최적의 세타를 이미 구했다면(뒤에서 살펴보자) 로지스틱 함수에 짚어넣는 선형식으로

결정 경계를 구할 수 있다. (맨 처음에 선형식이 안되는 이유를 말할 때를 보면 알 수 있다.)

결정 경계가 선형적이지 않으면 어떻게 구할 까?

선형 회귀에서 다항 회귀와 같이 feature에 n제곱을 취하여 복잡한 결정 경계를 구할 수 있다.

선형회귀 방식에서 비용함수는 이런 식을 사용하였다.

조금 더 간단하게 feature를 하나로 잡고 표현하면 이렇게 볼 수 있다.

그런데 애석하게도 로지스틱 함수는 "비선형"함수이기 때문에

이 비용함수의 합은 다음과 같이 나온다.

바로 왼쪽과 같이 나온다. local optima가 많아서 gradient descent를 하여도 global minimum에 도달할 보장이 없다.

비용함수의 합은 오른쪽과 같이 "볼록한" 그래프가 나와야 좋다.

그래서 로지스틱 회귀 방식에서는 다른 비용함수식을 사용한다.

바로 이 식이다. 이 cost함수 결과의 합이 최소화되면 된다.

(  0 < h(x) < 1 이므로 이 범위만 필요하다.)

h(x)값에 따라 조금 다르겠지만 이런 형태의 그래프가 그려진다.

y =0, y=1일때의 식이 다르므로 합치면 이런 모양이 된다.

최종 비용함수 J입니다.

Gradient descent는 선형회귀와 동일하게 진행합니다. 단지 hypothesis의 차이만 있을 뿐입니다.

지금까지는 yes or no 즉 2가지 분류에 대해서만 다루었다. 그럼 여러 종류의 분류는 어떻게 시행해야 할까?

바로 이런 프로세스로 시행한다.

세모, 네모, 엑스 로 분류할때

세모에 대한 hypothesis 1 (여기서는 Decision Boundary)

네모에 대한 hypothesis 2

엑스에 대한 hypothesis 3

을 각각 구하고 세로운 데이터가 들어올때

hθ(i)(x)= P(y=i | x; θ)을 구하고 가장 높은 확률의 값으로 분류하면 된다.

Linear Regression에서 gradient descent의 계산을 '벡터화'시켜서 행렬연산으로 만들자.

보통 저 시그마 연산을 for문으로 처리를 많이 한다.

그렇게 안하고 행렬연산으로 깔끔하게 할 수 있다.

먼저

이제 결과는 m X 1 의 행렬(열벡터)가 될 것이다.

결과행렬의 각 행에는 X의 j번째열의 i행을 곱한 뒤 모든 행을 더해주어야 한다.

그래서 X의 j번째열만을 추출한 행렬을 

이라 하자.

이제 

와 

의 각 행을 곱한 뒤 모두 더하면 된다.

두 행렬은 같은 m X 1의 행렬이므로 한 행렬의 전치 행렬을 취하여 행렬곱셈을 하면

각 행이 곱해진 뒤 모두 더해진다. 따라서

이번에는 선형 회귀 분석 알고리즘중 가장 간단한 Gradient Descent (경사 내려오기?)에 알아보자.

<그림 1>

위 그림 1처럼 현재 위치보다 작은곳으로 내려오는 알고리즘이다.

근데 위 곡면은 시작 위치에 따라 내려오는 지점이 다를 수 있다.

<그림 2-1>

그림 2-1의 내용이 Gradient descent 알고리즘의 과정이다.

" := " 은 대입연산자로써 프로그래밍 언어에서 " = "와 같다.

α는 learning rate로 얼마나 빨리 혹은 얼마나 느리게 내려올지를 정하는데 도움이 된다.

∂는 partial derivative(편미분) 기호이다.

수렴할때까지 진행하며 한번 수행시 모든 파라미터에대해(여기선 0~1) 수행한다.

<그림 2-2>

그림 2-1의 알고리즘 작성시 주의점은 그림 2-2의 오른쪽 처럼 하면은

세타0에 대입후 세타1에대해 계산시 세타0의 값이 달라져있기 때문에 바른값이 나오지 않으므로

주의해야 한다.

<그림 3-1>

그림 2-1의 알고리즘이 성립하는 이유를 살펴보자.

편의상 파라미터가 1개일때로 가정하자.

처음 세타값이 그림 3-1의 그래프처럼 최소점보다 오른쪽에 있을때

미분하면 양의 정수가 나올 것이다. 따라서

원래의 세타1에서 양수를 뺴므로 세타1은 작아진다.

작아지며 점점 최소점에 다가간다.

<그림 3-2>

반대로 세타값이 왼쪽에 있을때 미분하면 음수가 나온다.

음수를 빼면 더해지므로 세타값은 커진다.

커지며 점점 최소점에 다가간다.

<그림 4-1>

learning rate의 역할은 앞서 Gradient descent를 진행하며

빨리 내려올지 늦리게 내려올지를 결정한다고 하였다.

하지만 다른것도 그렇지만 항상 적당히가 중요하다.

learning rate값이 너무 작으면 그림4-1처럼 내려오는데 한참이 걸려

결과값을 얻는데 시간이 너무 오래 걸린다.

<그림 4-2>

반대로 너무 크면 그림 4-2처럼 내려오기는 커녕 오히려 위로 올라갈수도 있다.

그래서 적당량의 learning rate를 정해주는 것도 중요하다.

근데 learning rate를 계속 고정값으로 주어도 되는지 고민이 될 수도 있다.

최소점에 가까워질때마다 작게해주야할것같지만

다행히도 최소점에 가까워질수록 비용함수 J의 미분값이 0에 가까워지므로

세타의 증감량도 감소하므로 learning rate의 값을 변경하지 않아도 된다.

<그림 5>

위 그림 5에는 극소값이 2개가 있다.

그럼 만약 Gradient descent 진행 도중 그림 처럼 오른쪽 극소값을 만났을때 세타1의 증감은 어떻게 될까?

보시다시피 비용함수의 미분값이 0이 되므로 증감하지않고 멈추게 된다.

따라서 그림 1처럼 시작위치에 따라 얻는 결과가 다를 수 있는 문제가 있다.

<그림 6>

알고리즘에서 미분을 수행하여 그림 6의 아래처럼 식을 바꿀 수 있다.

Feature Scaling

<그림 7>

Gradient Descent시 결과값을 빠르게 취하기 위함이다.

변수들(크기, 화장실 수, 등등)의 범위를 대략 -1과 +1사이로 맞춘다.

위 수식 처럼 최대 크기로 나누어서 할 수 있으며

(avg는 해당 특성들의 평균)

이렇게도 할 수 있다. (현재 2번째 Scaling의 사용 이유를 잘 모르겠다. 아는 분은 코멘트좀 ㅠ)

Making sure gradient descent is working correctly

<그림 8>

그림 8처럼 gradient descent 반복 횟수에 따른 비용함수 크기가 증가하거나 일정구간을 반복될 경우

learning rate 값을 조금 줄일 필요가 있다.

Polynomial Regression

우리말로 다항 회귀 분석이라 한다.

<그림 9-1>

그림 9-1과 같은 그래프에서 최적의 직선을 구하여도

그래프의 점들이 직선보다는 곡선에 가깝게 분포하여 신뢰도가 떨어질 것이다.

그래서 polynomial regression은 최적의 곡선을 찾는다.

주로 2차나 3차곡선을 이용한다.

<그림 9-2>

그림 9-2의 2차곡선이 더 신뢰도가 있어보인다. 하지만 사이즈가 커지면 가격이

떨어질 수도 있다. (최대값 이후) 이 경우에는 밑의 9-3처럼 "루트"함수가 적합해 보인다.

<그림 9-3>

Normal Equation

<그림 10-1>

특성들이 있고 결과값이 있을때 행렬로 표현하면

이렇게 표현할 수 있다. (여기서 x0는 세타0과의 곱때문에 1로 둔다.)

결론 부터 위 방정식을 풀면 최적의 세타벡터를 얻을 수 있다.

식 도출)  위키백과

실제값과 hypothesis차이를 구하여

제곱의 합을 취하면 Cost Function과 같다. (앞서 보았던 cost function은 여기에 2m 나눔)

각 세타(여기 식에선 베타)에 대해 편미분하면

이고

이므로 다시쓰면

이다. Cost Function값이 최저일때 미분하면 0이므로

이렇게 쓸 수 있다. 식을 정리하면

이므로 행렬로 표현하면 

이되어 위 식을 구할 수 있다.

normal equation으로 반복작업 없이 바로 세타벡터를 구할 수 있지만 단점이 있다.

Gradient Descent와 비교하면

<그림 11>

normal equation은 learning rate값이 필요없으며

반복도 필요없는 장점이 있지만

계산비용이 커서 n(특성 개수)이 커지면 매우 느려진다.

Coursera강의에서는 n이 10000정도쯤 되면 Gradient Descent를 하는 것이 낫다고 한다.

비용 함수에 대해 더 살펴보자.

<그림 1-1>

그림 1-1의 hypothesis의 비용함수를 계산 하면

이므로 J(1) = 0 이다.

<그림 1-2>

그림 1-2의 hypothesis의 비용함수를 계산하면

J(0.5) = 약 0.69  가 나온다.

<그림 1-3>

그림 1-3의 비용함수를 계산하면

J(0) = 14/6 = 약 2.33  이 나온다.

<그림 2-1>

위 세타값들에 대한 비용함수 J의 값을 그래프에 그려보면 이렇게 나온다.

<그림 2-2>

그리고 모든 세타값들에 대한 비용함수 J의 값은 이런 곡선이 나올 것이다.

그리고 현재 세타가 1일때 J가 최저이므로

위 hypothesis에서 최적의 세타값은 1이다.

<그림 3-1>

집 가격문제로 돌아가서 집가격 문제의 경우 세타가 두개이다.

따라서 세타값들에 따른 비용함수 J의 값을 표시하면 그림 3-1과 같은

곡면이 나올 것이다.

<그림 3-2>

위 곡면을 보기 쉽게 등고선의 형태로 옮긴것이 그림 3-2의 오른쪽 그래프이다.

위 등고선을 보는 방법은 같은 선 위의 점들은 비용 함수의 값이 같다.

오른쪽 등고선위의 붉은 점(800, -1.5)일때 hypothesis의 그래프는 왼쪽 그래프이다.

아직 최적의 값이 아닌것 같다. 점을 옮겨보자.

<그림 3-3>

그림 3-3의 등고선의 붉은 점(360, 0)일때 아직은 미흡해보인다.

<그림 3-4>

그림 3-4의 등고선의 타원들의 중앙에 위치한 붉은점을때에 그래프가 최적으로 보인다.

저 붉은점이 그림 3-1에서 곡면의 가장 아래에 위치한 점이다.

위 내용이 선형 회귀 분석에서 일련의 과정이다.

파라미터가 위의 예처럼 1, 2개일때는 노가다로 찾을 수 있겠지만 현실은 파라미터가 수십 수백개일 것이다.

따라서 일련의 작업들을 특히 최적의 파라미터들을 찾는 작업을 자동으로 수행하게 하는 알고리즘이 필요하다.

이번에는 변수가 하나인 단순 선형 회귀를 살펴보자.

<그림1>

그림 1의 보라색 직선을 얻는 것이 최종 목표일 것이다.

위 모델에서 변수는 사이즈이다.

직선의 방정식은 y = b + ax 이므로 이를 바탕으로 식을 세운다.

이때의 식을 hypothesis 라 하며 (machine learning 분야에서 관습적으로 써왔다고 한다.)

간단하게 h(x)라고 표현하도록 한다.

이렇게 표현할 수 있다.

여기서 세타는 상수인데 현재 알지 못한다.

해서 세타값에 따라 이런 직선들이 그려진다.

<그림2>

<그림3>

따라서 위 그림3과 같은 모양이 나오는 최적의 세타0과 세타1을 찾는 것이 중요하다.

어떻게 해야 가장 공평한(?) 세타값을 찾을 수 있을까?

먼저 h(x)는 실제 가격 즉, 각 붉은 점들의 y값에 가까워야 한다는 것이다.

직선 위의 점들은     y - h(x)

직선 아래의 점들은  h(x) - y

를 모든 점( 데이터 셋 )에 대하여 수행한뒤 다 더하값이 최소화 될때 아마도 가장 최적화된 직선일 것이다.

이를 바탕으로 만든 식이 Cost Function 이다.

여기서 m은 데이터셋의 전체 데이터 수 이며, i는 각 데이터번호이며 그림1에서 집번호와 같다.

h(x) - y의 제곱을 취함으로써 음수를 배제하였고

1/2m을 곱한 이유는 찾아보니 미분시 편리함때문이고 나중에 나온다고 한다.

어쨌든 이 비용함수가 최소화 될때의 세타값을 취하면 된다.

What is Unsupervised Learning?

우리말로 비지도 학습이라하며

label이 없는 데이터가 입력으로 들어오는 경우에 해당한다.

Clustering

                         <그림 1>

위 그림 1과 같은 데이터셋이 주어질때 비슷한 특징을 갖는 "무리"를 빨간색 원과 같이 모아주는 것이다.

Supervised Learning - Classification 과 비슷하다.

"분류"를 한다는 점에서는 닮았지만 데이터에 label이 없어 분류하는 방식이 다르다.

그러기에 비슷한 데이터들을 엮어주는 역할만 한다.

사용자가 본 영화와 비슷한 영화를 추천해주거나 비슷한 이슈의 뉴스를 묶어서 보여준다는 등이 있다.