고귀양이의 노트.

레이 마칭 기본

2023. 6. 10. 21:30

레이 마칭 ( Ray Marching )을 통해 짧은 코드로도 제법 효과적인 ( 그럴듯한 ) 씬을 렌더 해보자.

작성된 데모 쉐이더 코드는 아래 링크를 통해 확인 할 수 있다.

https://www.shadertoy.com/view/mlcXWM

레이 마칭?

픽셀 별로 가상의 '광선'(Ray)을 카메라로부터 발사하고, 점진적으로 진행시켜서 물체에 닿았다고 판단되면 해당 물체의 색상( Color + Lighting )이 광선을 발사한 픽셀의 색으로 판단하는 기법이다.

일반적인 3D 렌더링 즉, 폴리곤(삼각형 집합)을 래스터라이징하여 렌더하는 것과는 사뭇 다른 방식의 렌더링 기법이다.

광선을 발사한다는 점에서는 레이 트레이싱(Ray Tracing)과 비슷하지만, 레이 트레이싱은 '점진적'으로 광선을 진행시키지 않고, 물체들의 표면을 돌며(씬에 오브젝트가 많다면 엄청 무겁다. 그래서 공간분할이 중요하다) 광선이 닿았는지 바로 검사하여 처리하는 방식으로 동작한다. 래스터라이징 방식의 렌더링에서는 폴리곤들의 표면 위치 정보가 있기 때문에 이런식으로 계산을 처리할 수 있다.

레이 마칭에서는 오브젝들의 표면 정보가 없기때문에, SDF( Signed Distance Function )이라 불리우는 거리 함수들을 통하여 물체의 표면을 판별하여 렌더한다.

그렇다면 레이 마칭은 복잡한 씬을 표현할 수 없는 걸까? 그런 당신에게 아래 링크를 선사한다.

볼때 마다 경이로움 : https://iquilezles.org/articles/raymarchingdf/

제노 블레이드 사례 : https://www.slideshare.net/leemwymw/2-ray-marching

설명에 앞서, 데모에서는 위 영상에서 보다시피, 2가지 shape의 거리함수를 사용하였다. 다른 다양한 shape들의 거리함수들 알고 싶다면 아래 링크를 확인.

3D SDF 레시피(경이로움 링크 주인) : https://iquilezles.org/articles/distfunctions/

데모 구현

그 전에 쉐이더 토이의 mainImage() 함수에 대해 알아야 한다. 복잡한 것은 없고, 픽셀 쉐이더(화면 픽셀마다 GPU에서 병렬로 실행되는 쉐이더 프로그램)이다. 따라서 픽셀의 색상을 적절히 반환하면 된다.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
	//...
}

반환할 픽셀 컬러는 fragColor에 넣으면 된다. fragCoord는 픽셀의 좌표인데, 단위와 방향은 다음과 같다.

[첨부3]의 빨간 부분에 적힌 해상도에 따른 각 픽셀의 좌표값이 fragCoord를 통해 전달된다. 주의할 것이 OpenGL에 익숙한 사람은 UV좌표의 방향과 같기때문에 상관없지만, DirectX에 익숙한 경우 Y방향이 헷갈릴 수 있다. ( Y가 아래방향이 커지는 방향.)

레이 생성

이제 fragCoord를 다음 코드 처럼 적절히 가공하여 픽셀별 광선을 생성할 수 있다.

// uv 좌표를 -1 ~ 1인 좌표로 만들고 z가 1인 레이를 만든다.
// 따라서, 수직수평 시야각이 90인 카메라 FOV가 된다.
vec2 uv = ((fragCoord * vec2(2, 2)) / iResolution.xy ) - vec2(1, 1);
vec3 rayDir = normalize(vec3(uv, 1));

이때, 카메라로부터 안쪽이 Z의 양수방향으로 하였다. ( DirextX 와 동일 )

정점계산이 없기 때문에, 좌표 구성은 입맛대로 해도 된다.

레이 진행

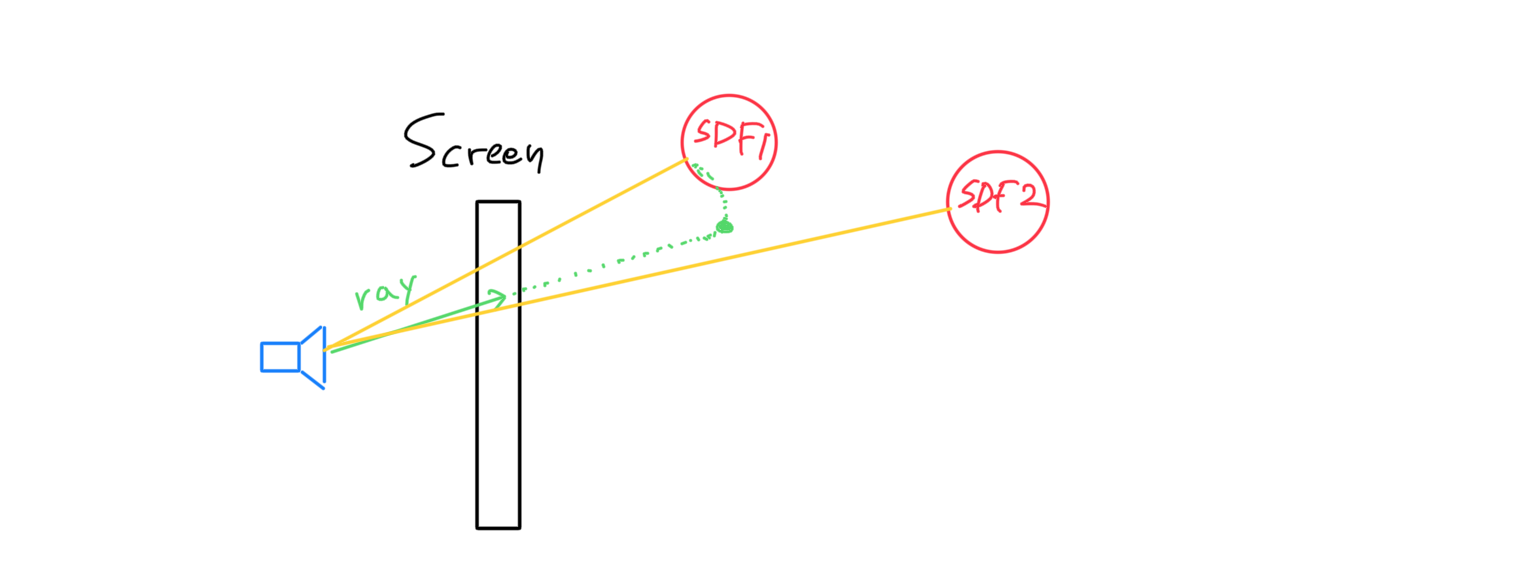
앞에서 얘기하였듯이, 앞서 구한 레이를 이제 점진적으로 진행시켜야 한다. 씬에 존재하는 물체들의 SDF 값을 비교하여 가장 작은 값(최단거리) 만큼 레이방향으로 전진시킨다.

전진 이후 아직 물체에 닿지 않았다면, 동일한 과정을 거쳐 레이를 진행시킨다. 이때 물체에 닿았다고 판단하는 방법은 SDF 값이 판별 거리 ( 아주 작은 값 ) 보다 작으면 닿은 것으로 간주하는 식으로 계산한다.

이 과정을 반복하다 보면, 언젠가 물체에 닿게 된다. 코드로 옮기면 다음과 같다.

RayResult rayMarch(vec3 ro, vec3 rd)
{
    // RO에서 현재까지 전진한 누적 거리 저장
    float dO = 0.;
    RayResult rr = RayResult(0.0, vec4(0.0), 0.0);
    
    int i = 0;
    for(; i < MAX_STEPS; i++)
    {
        vec3 p = ro + rd * dO;
        
        // GetDist() : 지정한 위치로부터 최단 SDF 거리값 계산
        rr = getDist(p);
        dO += rr._dist;              // 레이 전진
        
        // 하늘에 닿은 것( 최대 거리 )으로 간주
        if( dO > MAX_DIST )
            return RayResult(VERY_FAR, vec4(0.8, 0.9, 1.0, 1.0), 0.0);
            
        // 표면에 닿은 것으로 간주
        if( rr._dist < SURF_DIST)
            break;
    }
    
    rr._dist = dO;
    return rr;
}

코드에서 알 수 있듯, 레이가 허공을 향하는 경우 레이 진행이 안끝나기 때문에 무한루프를 돌 수 있다. 그래서MAX_STEPS 만큼만 진행한다. 또한, 진행 도중 너무 멀리가서 MAX_DIST보다 커지는 경우에도 미리 허공으로 간주하고 끝내버린다.

라이팅

레이 마칭을 통해 이제 물체의 표면 위치를 알게 되었다. ( camera position + ray direction * ray march distance 으로 구하면 알 수 있음 ) 이를 토대로 물체 표면의 라이팅을 계산하여 출력 색상을 결정하자.

float getLight(vec3 p)
{
    vec3 objectToLight = g_lightPos - p;
    vec3 L = normalize(objectToLight);
    vec3 N = getNormal(p);
    
    // Diffuse
    float diff = clamp( dot(N, L), 0.0, 1.0 );
    
    // Specular
    float specFactor = 0.0;
    if ( diff > 0.0 )
    {
        vec3 r = reflect(-L, N);
        vec3 toEye = normalize(g_cameraOrigin - p);
        specFactor = pow(max(dot(r, toEye), 0.0), 10.0);
    }
    
    // Shadow
    float d = rayMarch(p + L, L)._dist;
    if( d < length(objectToLight) )
        diff *= 0.3;
    
    return max(diff + specFactor, 0.15);
}

아주 특별한 것은 없다. Normal 벡터를 구하고, 미리 지정해둔 광원으로부터 Diffused Light와 Specular Light를 계산한다. ( 라이팅이 주제가 아니므로, 자세한 설명은 생략 )

여기서 중요한 것은 Shadow의 표현이다. 해당 표면으로부터 광원 방향으로 다시 한번 레이를 발사하여 구한 거리가 표면에서 광원까지의 거리보다 작다면 '응달'이라는 뜻으로, 해당 표면은 어둡게 표현해주면 단순한 그림자가 지게 된다.

반사

라이팅까지만 적용하여도 제법 그럴듯 하게 보인다. 거기에 추가적으로 간단한 반사까지 표현해주자.

vec4 getReflectedColor(vec3 p)
{
    vec3 cameraToObject = p - g_cameraOrigin;
    vec3 N = getNormal(p);
    
    vec3 reflectedRayDir = reflect(normalize(cameraToObject), N);
    
    RayResult rr = rayMarch(p + reflectedRayDir, reflectedRayDir);
    return rr._color;
}

카메라에서 표면으로 가는 벡터를 Normal 벡터에 반사시킨 벡터 reflectedRayDir를 구한뒤, 표면으로부터 해당 방향으로 레이를 쏴서 구해지는 물체의 색상을 반환한다.

( 조금 더 사실적으로 하려면 추가적으로 라이팅을 계산해야 한다. 하지만 원리를 이제 알았으니 귀찮아서 패스 )

최종

이렇게 구해진 색상, 1차반사 색상, 라이팅 등을 섞어서 최종 색상으로 반환한다.

// 픽셀의 거리 계산
RayResult rr = rayMarch(g_cameraOrigin, rayDir);
if (rr._dist >= VERY_FAR)
{
    // 하늘
    fragColor = rr._color;
    return;
}
    
// 광원으로부터 light 계산
float diff = getLight(g_cameraOrigin + (rayDir * rr._dist));
       
// 물체 위치로부터 1차 반사 계산
vec4 reflectedColor = getReflectedColor(g_cameraOrigin + (rayDir * rr._dist));
        
// color + reflect color
fragColor = (1.0 - rr._reflectRatio) * rr._color + rr._reflectRatio * reflectedColor;
    
// + light
fragColor = clamp(fragColor * diff, 0.0, 1.0);

위에서 설명하지는 않았지만, 쉐이더 토이에서 키보드 입력을 처리하는 방법은 아래 링크의 코드를 참고하면 알 수 있다.

https://www.shadertoy.com/view/ltsyRS

간단하게 설명하자면, Buffer A로 렌더하는 쉐이더를 하나 더 추가하고, 키보드 버퍼에서 값을 읽어서 Buffer A의 키별 특정 위치에 누적시킨다. 실제 키보드 입력에 따라 동작을 하는 쉐이더에서는 Buffer A의 누적값을 읽어서 처리한다.